
Linear models#
Basics of modeling, optimization, and regularization
Mahmood Amintoosi, Spring 2025
Computer Science Dept, Ferdowsi University of Mashhad
I should mention that the original material of this course was from Open Machine Learning Course, by Joaquin Vanschoren and others.
Show code cell source
# Auto-setup when running on Google Colab
import os
if 'google.colab' in str(get_ipython()) and not os.path.exists('/content/machine-learning'):
!git clone -q https://github.com/fum-cs/machine-learning.git /content/machine-learning
!pip --quiet install -r /content/machine-learning/requirements_colab.txt
%cd machine-learning/notebooks
# Global imports and settings
%matplotlib inline
from preamble import *
interactive = False # Set to True for interactive plots
if interactive:
fig_scale = 0.5
plt.rcParams.update(print_config)
else: # For printing
fig_scale = 0.3
plt.rcParams.update(print_config)
Notation and Definitions#
A scalar is a simple numeric value, denoted by an italic letter: \(x=3.24\)
A vector is a 1D ordered array of n scalars, denoted by a bold letter: \(\mathbf{x}=[3.24, 1.2]\)
\(x_i\) denotes the \(i\)th element of a vector, thus \(x_0 = 3.24\).
Note: some other courses use \(x^{(i)}\) notation
A set is an unordered collection of unique elements, denote by caligraphic capital: \(\mathcal{S}=\{3.24, 1.2\}\)
A matrix is a 2D array of scalars, denoted by bold capital: \(\mathbf{X}=\begin{bmatrix} 3.24 & 1.2 \\ 2.24 & 0.2 \end{bmatrix}\)
\(\textbf{X}_{i}\) denotes the \(i\)th row of the matrix
\(\textbf{X}_{:,j}\) denotes the \(j\)th column
\(\textbf{X}_{i,j}\) denotes the element in the \(i\)th row, \(j\)th column, thus \(\mathbf{X}_{1,0} = 2.24\)
\(\mathbf{X}^{n \times p}\), an \(n \times p\) matrix, can represent \(n\) data points in a \(p\)-dimensional space
Every row is a vector that can represent a point in an p-dimensional space, given a basis.
The standard basis for a Euclidean space is the set of unit vectors
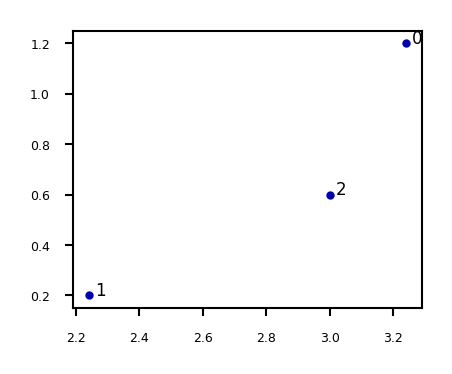
E.g. if \(\mathbf{X}=\begin{bmatrix} 3.24 & 1.2 \\ 2.24 & 0.2 \\ 3.0 & 0.6 \end{bmatrix}\)
Show code cell source
X = np.array([[3.24 , 1.2 ],[2.24, 0.2],[3.0 , 0.6 ]])
fig = plt.figure(figsize=(5*fig_scale,4*fig_scale))
plt.scatter(X[:,0],X[:,1])
for i in range(3):
plt.annotate(i, (X[i,0]+0.02, X[i,1]))
A tensor is an k-dimensional array of data, denoted by an italic capital: \(T\)
k is also called the order, degree, or rank
\(T_{i,j,k,...}\) denotes the element or sub-tensor in the corresponding position
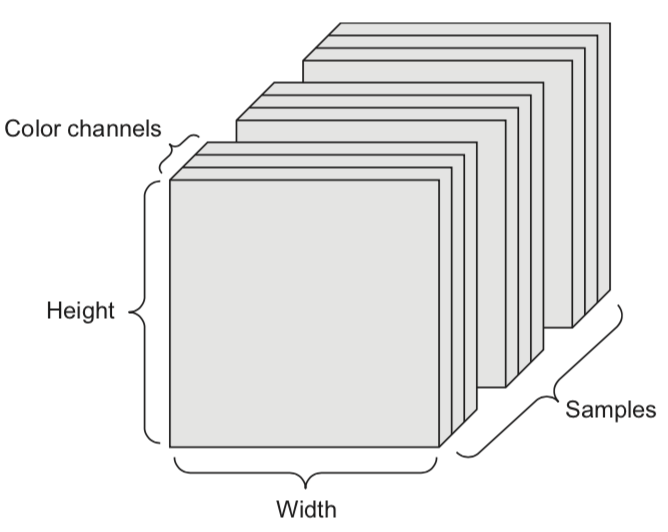
A set of color images can be represented by:
a 4D tensor (sample x height x width x color channel)
a 2D tensor (sample x flattened vector of pixel values)
Basic operations#
Sums and products are denoted by capital Sigma and capital Pi:
Operations on vectors are element-wise: e.g. \(\mathbf{x}+\mathbf{z} = [x_0+z_0,x_1+z_1, ... , x_p+z_p]\)
Dot product \(\mathbf{w}\mathbf{x} = \mathbf{w} \cdot \mathbf{x} = \mathbf{w}^{T} \mathbf{x} = \sum_{i=0}^{p} w_i \cdot x_i = w_0 \cdot x_0 + w_1 \cdot x_1 + ... + w_p \cdot x_p\)
Matrix product \(\mathbf{W}\mathbf{x} = \begin{bmatrix} \mathbf{w_0} \cdot \mathbf{x} \\ ... \\ \mathbf{w_p} \cdot \mathbf{x} \end{bmatrix}\)
A function \(f(x) = y\) relates an input element \(x\) to an output \(y\)
It has a local minimum at \(x=c\) if \(f(x) \geq f(c)\) in interval \((c-\epsilon, c+\epsilon)\)
It has a global minimum at \(x=c\) if \(f(x) \geq f(c)\) for any value for \(x\)
A vector function consumes an input and produces a vector: \(\mathbf{f}(\mathbf{x}) = \mathbf{y}\)
\(\underset{x\in X}{\operatorname{max}}f(x)\) returns the largest value f(x) for any x
\(\underset{x\in X}{\operatorname{argmax}}f(x)\) returns the element x that maximizes f(x)
Gradients#
A derivative \(f'\) of a function \(f\) describes how fast \(f\) grows or decreases
The process of finding a derivative is called differentiation
Derivatives for basic functions are known
For non-basic functions we use the chain rule: \(F(x) = f(g(x)) \rightarrow F'(x)=f'(g(x))g'(x)\)
A function is differentiable if it has a derivative in any point of it’s domain
It’s continuously differentiable if \(f'\) is a continuous function
We say \(f\) is smooth if it is infinitely differentiable, i.e., \(f', f'', f''', ...\) all exist
A gradient \(\nabla f\) is the derivative of a function in multiple dimensions
It is a vector of partial derivatives: \(\nabla f = \left[ \frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1},... \right]\)
E.g. \(f=2x_0+3x_1^{2}-\sin(x_2) \rightarrow \nabla f= [2, 6x_1, -cos(x_2)]\)
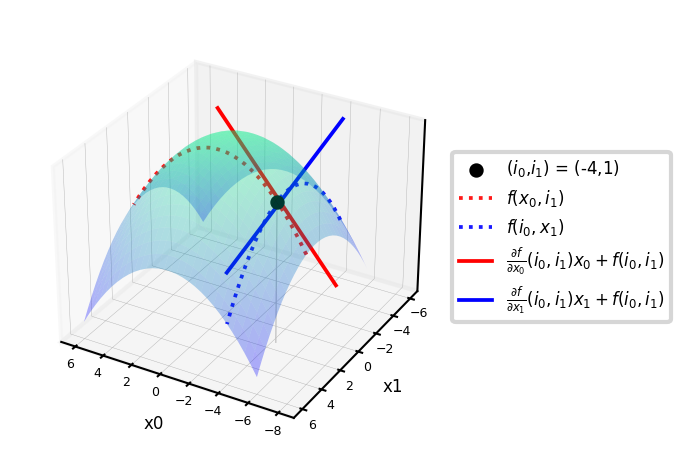
Example: \(f = -(x_0^2+x_1^2)\)
\(\nabla f = \left[\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1}\right] = \left[-2x_0,-2x_1\right]\)
Evaluated at point (-4,1): \(\nabla f(-4,1) = [8,-2]\)
These are the slopes at point (-4,1) in the direction of \(x_0\) and \(x_1\) respectively
Show code cell source
from mpl_toolkits import mplot3d
import ipywidgets as widgets
from ipywidgets import interact, interact_manual
# f = -(x0^2 + x1^2)
def g_f(x0, x1):
return -(x0 ** 2 + x1 ** 2)
def g_dfx0(x0):
return -2 * x0
def g_dfx1(x1):
return -2 * x1
@interact
def plot_gradient(rotation=(0,240,10)):
# plot surface of f
fig = plt.figure(figsize=(12*fig_scale,5*fig_scale))
ax = plt.axes(projection="3d")
x0 = np.linspace(-6, 6, 30)
x1 = np.linspace(-6, 6, 30)
X0, X1 = np.meshgrid(x0, x1)
ax.plot_surface(X0, X1, g_f(X0, X1), rstride=1, cstride=1,
cmap='winter', edgecolor='none',alpha=0.3)
# choose point to evaluate: (-4,1)
i0 = -4
i1 = 1
iz = np.linspace(g_f(i0,i1), -82, 30)
ax.scatter3D(i0, i1, g_f(i0,i1), c="k", s=20*fig_scale,label='($i_0$,$i_1$) = (-4,1)')
ax.plot3D([i0]*30, [i1]*30, iz, linewidth=1*fig_scale, c='silver', linestyle='-')
ax.set_zlim(-80,0)
# plot intersects
ax.plot3D(x0,[1]*30,g_f(x0, 1),linewidth=3*fig_scale,alpha=0.9,label='$f(x_0,i_1)$',c='r',linestyle=':')
ax.plot3D([-4]*30,x1,g_f(-4, x1),linewidth=3*fig_scale,alpha=0.9,label='$f(i_0,x_1)$',c='b',linestyle=':')
# df/dx0 is slope of line at the intersect point
x0 = np.linspace(-8, 0, 30)
ax.plot3D(x0,[1]*30,g_dfx0(i0)*x0-g_f(i0,i1),linewidth=3*fig_scale,label=r'$\frac{\partial f}{\partial x_0}(i_0,i_1) x_0 + f(i_0,i_1)$',c='r',linestyle='-')
ax.plot3D([-4]*30,x1,g_dfx1(i1)*x1+g_f(i0,i1),linewidth=3*fig_scale,label=r'$\frac{\partial f}{\partial x_1}(i_0,i_1) x_1 + f(i_0,i_1)$',c='b',linestyle='-')
ax.set_xlabel('x0', labelpad=-4/fig_scale)
ax.set_ylabel('x1', labelpad=-4/fig_scale)
ax.get_zaxis().set_ticks([])
ax.view_init(30, rotation) # Use this to rotate the figure
ax.legend()
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.tick_params(axis='both', width=0, labelsize=10*fig_scale, pad=-6)
plt.tight_layout()
plt.show()
Show code cell source
if not interactive:
plot_gradient(rotation=120)
Distributions and Probabilities#
The normal (Gaussian) distribution with mean \(\mu\) and standard deviation \(\sigma\) is noted as \(N(\mu,\sigma)\)
A random variable \(X\) can be continuous or discrete
A probability distribution \(f_X\) of a continuous variable \(X\): probability density function (pdf)
The expectation is given by \(\mathbb{E}[X] = \int x f_{X}(x) dx\)
A probability distribution of a discrete variable: probability mass function (pmf)
The expectation (or mean) \(\mu_X = \mathbb{E}[X] = \sum_{i=1}^k[x_i \cdot Pr(X=x_i)]\)

Linear models#
Linear models make a prediction using a linear function of the input features \(X\)
Learn \(w\) from \(X\), given a loss function \(\mathcal{L}\):
Many algorithms with different \(\mathcal{L}\): Least squares, Ridge, Lasso, Logistic Regression, Linear SVMs,…
Can be very powerful (and fast), especially for large datasets with many features.
Can be generalized to learn non-linear patterns: Generalized Linear Models
Features can be augmentented with polynomials of the original features
Features can be transformed according to a distribution (Poisson, Tweedie, Gamma,…)
Some linear models (e.g. SVMs) can be kernelized to learn non-linear functions
Linear models for regression#
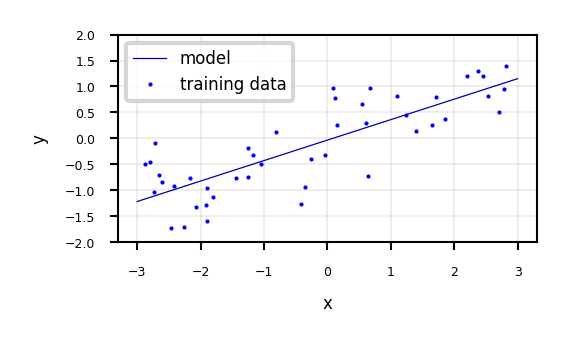
Prediction formula for input features x:
\(w_1\) … \(w_p\) usually called weights or coefficients , \(w_0\) the bias or intercept
Assumes that errors are \(N(0,\sigma)\)
Show code cell source
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from mglearn.datasets import make_wave
Xw, yw = make_wave(n_samples=60)
Xw_train, Xw_test, yw_train, yw_test = train_test_split(Xw, yw, random_state=42)
line = np.linspace(-3, 3, 100).reshape(-1, 1)
lr = LinearRegression().fit(Xw_train, yw_train)
print("w_1: %f w_0: %f" % (lr.coef_[0], lr.intercept_))
plt.figure(figsize=(6*fig_scale, 3*fig_scale))
plt.plot(line, lr.predict(line), lw=fig_scale)
plt.plot(Xw_train, yw_train, 'o', c='b')
#plt.plot(X_test, y_test, '.', c='r')
ax = plt.gca()
ax.grid(True)
ax.set_ylim(-2, 2)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(["model", "training data"], loc="best");
w_1: 0.393906 w_0: -0.031804
Linear Regression (aka Ordinary Least Squares)#
Loss function is the sum of squared errors (SSE) (or residuals) between predictions \(\hat{y}_i\) (red) and the true regression targets \(y_i\) (blue) on the training set.
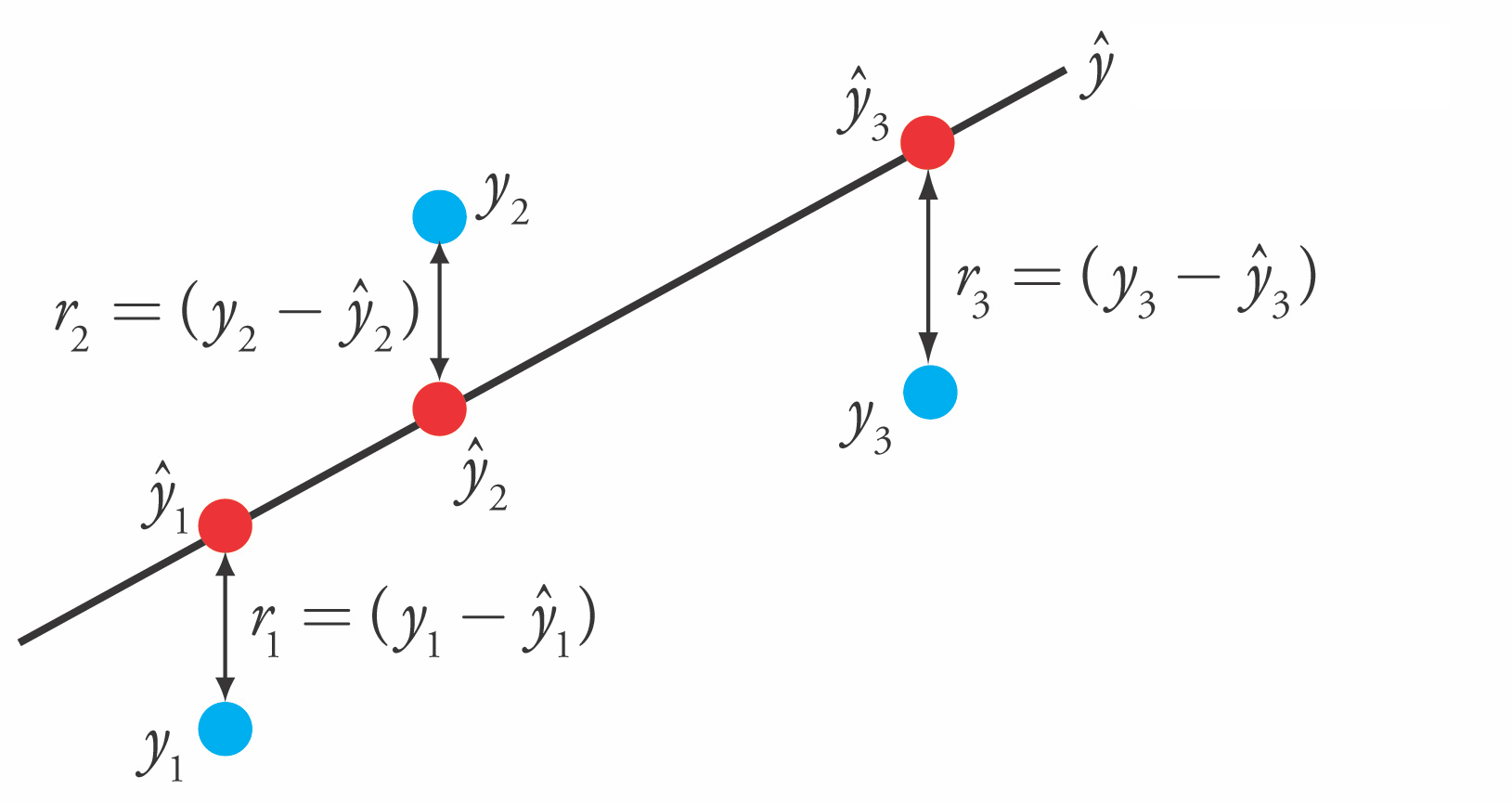
Solving ordinary least squares#
Closed-Form Solution
Convex optimization problem with unique closed-form solution:
\[w^{*} = (X^{T}X)^{-1} X^T \mathbf{y}\]Add a column of 1’s to the front of X to get \(w_0\)
Slow. Time complexity is quadratic in number of features: \(\mathcal{O}(p^2n)\)
X has \(n\) rows, \(p\) features, hence \(X^{T}X\) has dimensionality \(p \cdot p\)
Only works if \(n>p\)
Overfitting Risks of Closed-Form Solution
The closed-form solution of Ordinary Least Squares (OLS) is highly prone to overfitting, especially when applied to small or highly correlated datasets.
Large coefficients: In the absence of regularization, weights \( w \) can grow excessively, leading to unstable predictions.
Sensitive to input variations: Small changes in \( x \) may result in disproportionately large shifts in the output \( y \), making the model unreliable.
No direct hyperparameter control: Unlike Gradient Descent, OLS lacks tuning mechanisms such as learning rate or regularization strength.
Gradient Descent
More efficient for large-scale or high-dimensional datasets.
Preferred when computing \( X^{T}X \) is infeasible or excessively time-consuming due to large \( p \) or \( n \).
Offers multiple tunable settings to control the learning process, including:
Learning Rate: Adjusts update speed to balance stability and convergence.
Regularization: Options like L1, L2, or Elastic Net mitigate overfitting.
Batch Size: Influences computational efficiency (Stochastic, Mini-batch, Full-batch).
Iterations: Determines the number of passes over the dataset.
Momentum & Decay: Helps stabilize and refine the learning trajectory.
Why \( X^T X \) is Singular When \( n < p \)?#
For a design matrix \( X \in \mathbb{R}^{n \times p} \):
Rank Constraint:
\(\text{rank}(X) \leq \min(n, p)\).
If \( n < p \), \(\text{rank}(X) \leq n < p \), so \( X \) is column-rank-deficient.
Gram Matrix \( X^T X \):
\( X^T X \in \mathbb{R}^{p \times p} \) has the same rank as \( X \):
\[ \text{rank}(X^T X) = \text{rank}(X) < p. \]Thus, \( X^T X \) is singular (non-invertible).
Null Space Argument:
\(\text{null}(X) = \text{null}(X^T X)\) (since \( X^T X \mathbf{v} = 0 \iff X \mathbf{v} = 0 \)).
If \( n < p \), \(\text{nullity}(X) = p - \text{rank}(X) \geq p - n > 0 \), meaning there exist non-zero \( \mathbf{v} \) such that \( X^T X \mathbf{v} = 0 \).
Geometric Intuition:
\( X \) maps \( \mathbb{R}^p \to \mathbb{R}^n \) with \( p > n \), implying linear dependence in its columns.
\( X^T X \)’s singularity reflects this dependence, making OLS’s \( (X^T X)^{-1} \) undefined.
Implications:
OLS fails: \( \mathbf{w}^* = (X^T X)^{-1} X^T \mathbf{y} \) cannot be computed.
Solutions:
Regularization: Ridge Regression adds \( \lambda I \) to ensure invertibility.
Dimensionality Reduction: Use PCA or feature selection to reduce \( p \).
For further information please See [Bak18].
Show code cell source
import numpy as np
# Example with n=2, p=3 (n < p)
X = np.array([[1, 2, 3],
[4, 5, 6]]) # 2x3 matrix (n=2, p=3)
# Compute X^T X
XTX = np.dot(X.T, X) # or X.T @ X
print("X (design matrix):")
print(X)
print("\nX^T X (Gram matrix):")
print(XTX)
# Check singularity
rank_X = np.linalg.matrix_rank(X)
rank_XTX = np.linalg.matrix_rank(XTX)
is_singular = rank_XTX < XTX.shape[0] # True if singular
print("\nRank of X:", rank_X)
print("Rank of X^T X:", rank_XTX)
print("Is X^T X singular?", is_singular)
# Attempt to invert (will fail)
try:
np.linalg.inv(XTX)
except np.linalg.LinAlgError:
print("\nError: X^T X is singular and cannot be inverted (as expected when n < p).")
X (design matrix):
[[1 2 3]
[4 5 6]]
X^T X (Gram matrix):
[[17 22 27]
[22 29 36]
[27 36 45]]
Rank of X: 2
Rank of X^T X: 2
Is X^T X singular? True
Error: X^T X is singular and cannot be inverted (as expected when n < p).
Gradient Descent#
Start with an initial, random set of weights: \(\mathbf{w}^0\)
Given a differentiable loss function \(\mathcal{L}\) (e.g. \(\mathcal{L}_{SSE}\)), compute \(\nabla \mathcal{L}\)
For least squares: \(\frac{\partial \mathcal{L}_{SSE}}{\partial w_i}(\mathbf{w}) = -2\sum_{n=1}^{N} (y_n-\hat{y}_n) x_{n,i}\)
If feature \(X_{:,i}\) is associated with big errors, the gradient wrt \(w_i\) will be large
Update all weights slightly (by step size or learning rate \(\eta\)) in ‘downhill’ direction.
Basic update rule (step s):
\[\mathbf{w}^{s+1} = \mathbf{w}^s-\eta\nabla \mathcal{L}(\mathbf{w}^s)\]
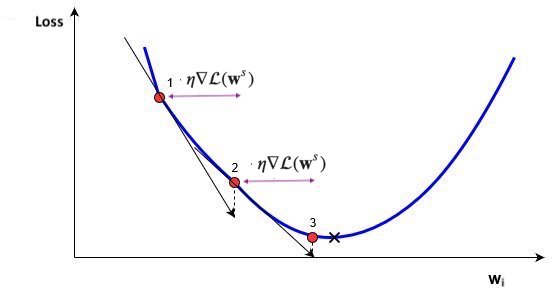
Important hyperparameters
Learning rate
Too small: slow convergence. Too large: possible divergence
Maximum number of iterations
Too small: no convergence. Too large: wastes resources
Learning rate decay with decay rate \(k\)
E.g. exponential (\(\eta^{s+1} = \eta^{0} e^{-ks}\)), inverse-time (\(\eta^{s+1} = \frac{\eta^{s}}{1+ks}\)),…
Many more advanced ways to control learning rate (see later)
Adaptive techniques: depend on how much loss improved in previous step
Show code cell source
import math
# Some convex function to represent the loss
def l_fx(x):
return (x * 4)**2
# Derivative to compute the gradient
def l_dfx0(x0):
return 8 * x0
@interact
def plot_learning_rate(learn_rate=(0.01,0.4,0.01), exp_decay=False):
w = np.linspace(-1,1,101)
f = [l_fx(i) for i in w]
w_current = -0.75
learn_rate_current = learn_rate
fw = [] # weight values
fl = [] # loss values
for i in range(10):
fw.append(w_current)
fl.append(l_fx(w_current))
# Decay
if exp_decay:
learn_rate_current = learn_rate * math.exp(-0.3*i)
# Update rule
w_current = w_current - learn_rate_current * l_dfx0(w_current)
fig, ax = plt.subplots(figsize=(5*fig_scale,3*fig_scale))
ax.set_xlabel('w')
ax.set_xticks([])
ax.set_ylabel('loss')
ax.plot(w, f, lw=2*fig_scale, ls='-', c='k', label='Loss')
ax.plot(fw, fl, '--bo', lw=2*fig_scale, markersize=3)
plt.ylim(-1,16)
plt.xlim(-1,1)
Show code cell output
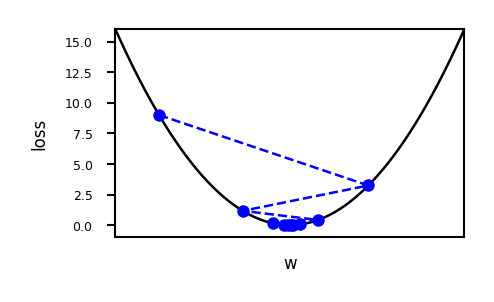
Show code cell source
if not interactive:
plot_learning_rate(learn_rate=0.21, exp_decay=False)
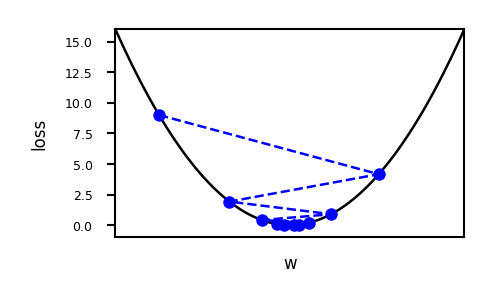
Show code cell source
import tensorflow as tf
# import tensorflow_addons as tfa
# Toy surface
def f(x, y):
return (1.5 - x + x*y)**2 + (2.25 - x + x*y**2)**2 + (2.625 - x + x*y**3)**2
# Tensorflow optimizers
sgd = tf.optimizers.SGD(0.01)
lr_schedule = tf.optimizers.schedules.ExponentialDecay(0.02,decay_steps=100,decay_rate=0.96)
sgd_decay = tf.optimizers.SGD(learning_rate=lr_schedule)
optimizers = [sgd, sgd_decay]
opt_names = ['sgd', 'sgd_decay']
cmap = plt.cm.get_cmap('tab10')
colors = [cmap(x/10) for x in range(10)]
# Training
all_paths = []
for opt, name in zip(optimizers, opt_names):
x = tf.Variable(0.8)
y = tf.Variable(1.6)
x_history = []
y_history = []
loss_prev = 0.0
max_steps = 100
for step in range(max_steps):
with tf.GradientTape() as g:
loss = f(x, y)
x_history.append(x.numpy())
y_history.append(y.numpy())
grads = g.gradient(loss, [x, y])
opt.apply_gradients(zip(grads, [x, y]))
if np.abs(loss_prev - loss.numpy()) < 1e-6:
break
loss_prev = loss.numpy()
x_history = np.array(x_history)
y_history = np.array(y_history)
path = np.concatenate((np.expand_dims(x_history, 1), np.expand_dims(y_history, 1)), axis=1).T
all_paths.append(path)
Show code cell source
from matplotlib.colors import LogNorm
import tensorflow as tf
# Toy surface
def f(x, y):
return (1.5 - x + x*y)**2 + (2.25 - x + x*y**2)**2 + (2.625 - x + x*y**3)**2
# Tensorflow optimizers
sgd = tf.optimizers.SGD(0.01)
lr_schedule = tf.optimizers.schedules.ExponentialDecay(0.02,decay_steps=100,decay_rate=0.96)
sgd_decay = tf.optimizers.SGD(learning_rate=lr_schedule)
optimizers = [sgd, sgd_decay]
opt_names = ['sgd', 'sgd_decay']
cmap = plt.cm.get_cmap('tab10')
colors = [cmap(x/10) for x in range(10)]
# Training
all_paths = []
for opt, name in zip(optimizers, opt_names):
x_init = 0.8
x = tf.Variable(x_init)
y_init = 1.6
y = tf.Variable(y_init)
x_history = []
y_history = []
z_prev = 0.0
max_steps = 100
for step in range(max_steps):
with tf.GradientTape() as g:
z = f(x, y)
x_history.append(x.numpy())
y_history.append(y.numpy())
dz_dx, dz_dy = g.gradient(z, [x, y])
opt.apply_gradients(zip([dz_dx, dz_dy], [x, y]))
if np.abs(z_prev - z.numpy()) < 1e-6:
break
z_prev = z.numpy()
x_history = np.array(x_history)
y_history = np.array(y_history)
path = np.concatenate((np.expand_dims(x_history, 1), np.expand_dims(y_history, 1)), axis=1).T
all_paths.append(path)
# Plotting
number_of_points = 50
margin = 4.5
minima = np.array([3., .5])
minima_ = minima.reshape(-1, 1)
x_min = 0. - 2
x_max = 0. + 3.5
y_min = 0. - 3.5
y_max = 0. + 2
x_points = np.linspace(x_min, x_max, number_of_points)
y_points = np.linspace(y_min, y_max, number_of_points)
x_mesh, y_mesh = np.meshgrid(x_points, y_points)
z = np.array([f(xps, yps) for xps, yps in zip(x_mesh, y_mesh)])
def plot_optimizers(ax, iterations, optimizers):
ax.contour(x_mesh, y_mesh, z, levels=np.logspace(-0.5, 5, 25), norm=LogNorm(), cmap=plt.cm.jet, linewidths=fig_scale, zorder=-1)
ax.plot(*minima, 'r*', markersize=20*fig_scale)
for name, path, color in zip(opt_names, all_paths, colors):
if name in optimizers:
p = path[:,:iterations]
ax.plot([], [], color=color, label=name, lw=3*fig_scale, linestyle='-')
ax.quiver(p[0,:-1], p[1,:-1], p[0,1:]-p[0,:-1], p[1,1:]-p[1,:-1], scale_units='xy', angles='xy', scale=1, color=color, lw=4)
ax.set_xlim((x_min, x_max))
ax.set_ylim((y_min, y_max))
ax.legend(loc='lower left', prop={'size': 15*fig_scale})
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
Show code cell source
from decimal import *
# Training for momentum
all_lr_paths = []
lr_range = [0.005 * i for i in range(0,10)]
for lr in lr_range:
opt = tf.optimizers.SGD(lr, nesterov=False)
x_init = 0.8
x = tf.compat.v1.get_variable('x', dtype=tf.float32, initializer=tf.constant(x_init))
y_init = 1.6
y = tf.compat.v1.get_variable('y', dtype=tf.float32, initializer=tf.constant(y_init))
x_history = []
y_history = []
z_prev = 0.0
max_steps = 100
for step in range(max_steps):
with tf.GradientTape() as g:
z = f(x, y)
x_history.append(x.numpy())
y_history.append(y.numpy())
dz_dx, dz_dy = g.gradient(z, [x, y])
opt.apply_gradients(zip([dz_dx, dz_dy], [x, y]))
if np.abs(z_prev - z.numpy()) < 1e-6:
break
z_prev = z.numpy()
x_history = np.array(x_history)
y_history = np.array(y_history)
path = np.concatenate((np.expand_dims(x_history, 1), np.expand_dims(y_history, 1)), axis=1).T
all_lr_paths.append(path)
# Plotting
number_of_points = 50
margin = 4.5
minima = np.array([3., .5])
minima_ = minima.reshape(-1, 1)
x_min = 0. - 2
x_max = 0. + 3.5
y_min = 0. - 3.5
y_max = 0. + 2
x_points = np.linspace(x_min, x_max, number_of_points)
y_points = np.linspace(y_min, y_max, number_of_points)
x_mesh, y_mesh = np.meshgrid(x_points, y_points)
z = np.array([f(xps, yps) for xps, yps in zip(x_mesh, y_mesh)])
def plot_learning_rate_optimizers(ax, iterations, lr):
ax.contour(x_mesh, y_mesh, z, levels=np.logspace(-0.5, 5, 25), norm=LogNorm(), cmap=plt.cm.jet, linewidths=fig_scale, zorder=-1)
ax.plot(*minima, 'r*', markersize=20*fig_scale)
for path, lrate in zip(all_lr_paths, lr_range):
if round(lrate,3) == lr:
p = path[:,:iterations]
ax.plot([], [], color='b', label="Learning rate {}".format(lr), lw=3*fig_scale, linestyle='-')
ax.quiver(p[0,:-1], p[1,:-1], p[0,1:]-p[0,:-1], p[1,1:]-p[1,:-1], scale_units='xy', angles='xy', scale=1, color='b', lw=4)
ax.set_xlim((x_min, x_max))
ax.set_ylim((y_min, y_max))
ax.legend(loc='lower left', prop={'size': 15*fig_scale})
ax.set_xticks([])
ax.set_yticks([])
plt.tight_layout()
WARNING:tensorflow:From C:\Users\mamin\AppData\Local\Temp\ipykernel_17912\2027666145.py:10: The name tf.get_variable is deprecated. Please use tf.compat.v1.get_variable instead.
Effect of learning rate
Show code cell source
@interact
def plot_lr(iterations=(1,100,1), learning_rate=(0.01,0.04,0.005)):
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
plot_learning_rate_optimizers(ax,iterations,learning_rate)
if not interactive:
plot_lr(iterations=50, learning_rate=0.02)
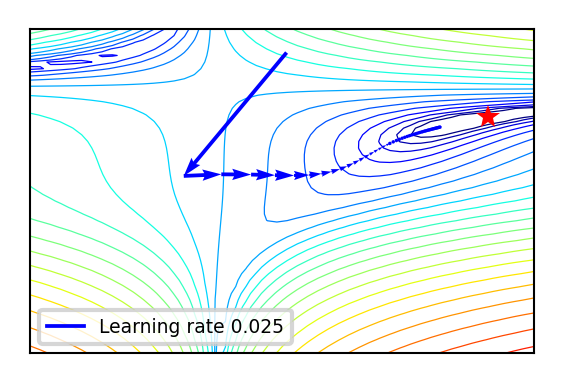

Effect of learning rate decay
Show code cell source
@interact
def compare_optimizers(iterations=(1,100,1), optimizer1=opt_names, optimizer2=opt_names):
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
plot_optimizers(ax,iterations,[optimizer1,optimizer2])
if not interactive:
compare_optimizers(iterations=50, optimizer1="sgd", optimizer2="sgd_decay")
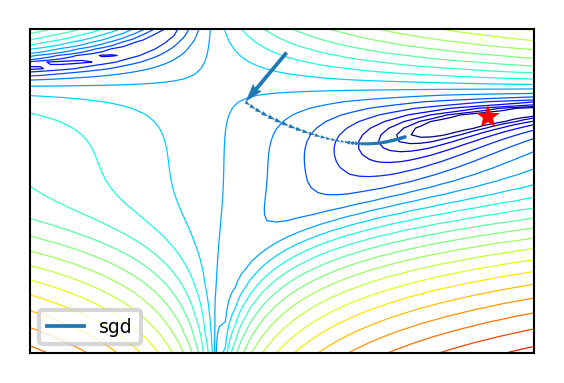
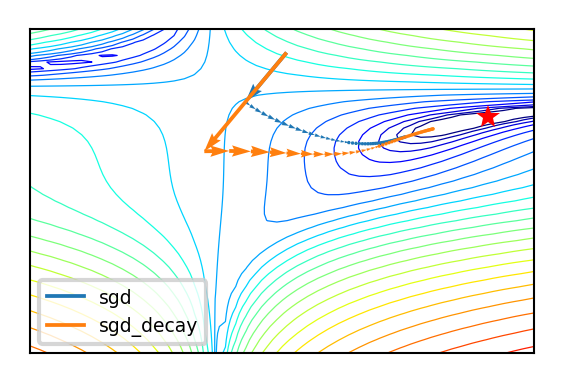
In two dimensions:
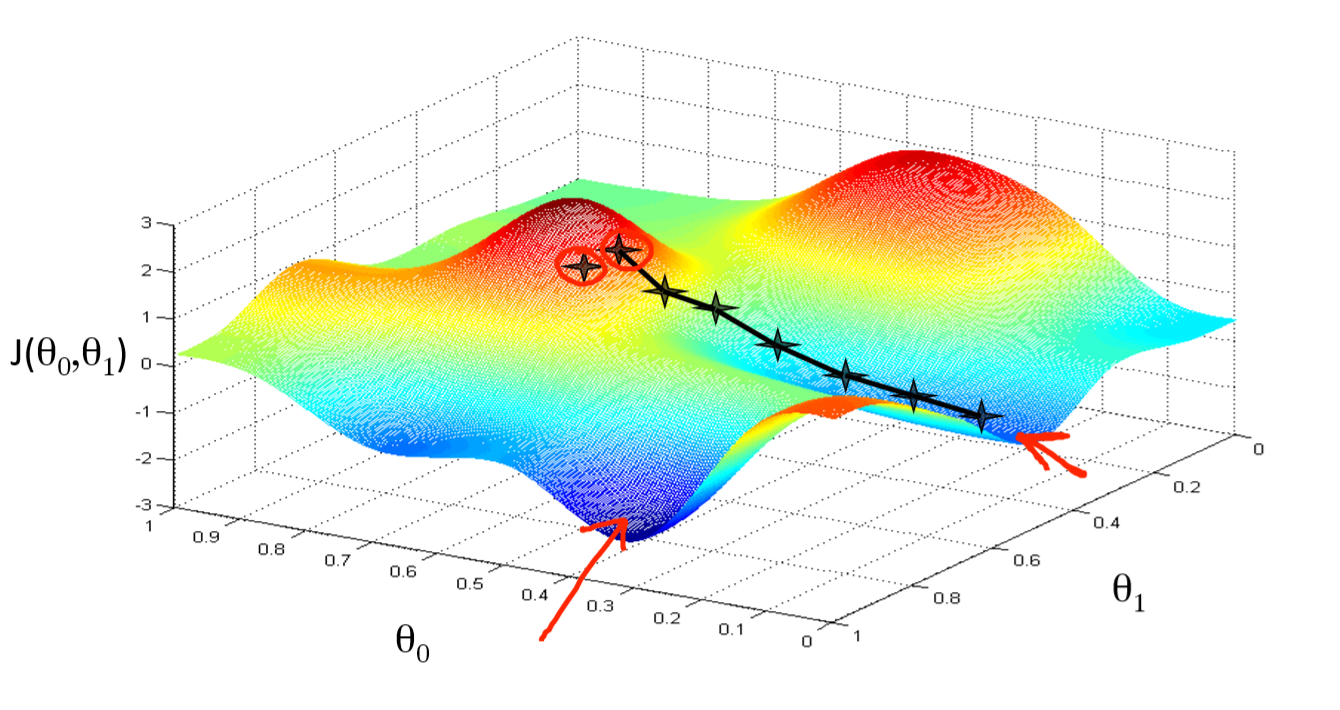
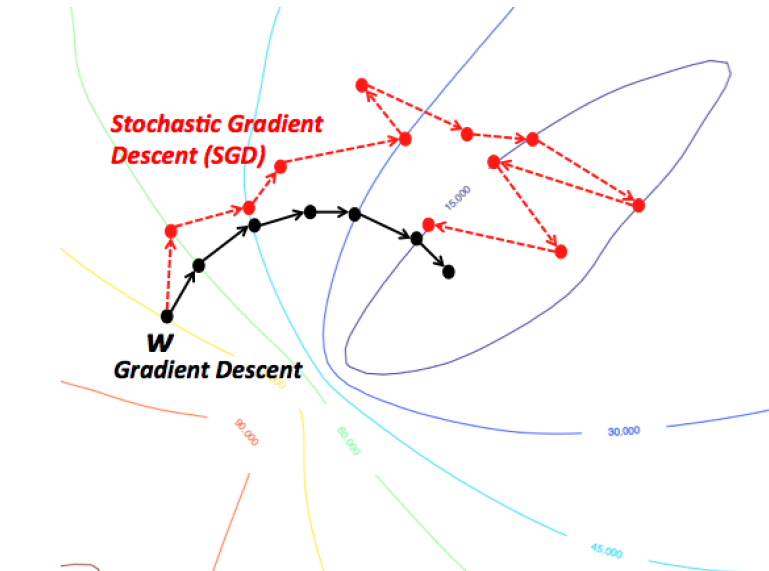
You can get stuck in local minima (if the loss is not fully convex)
If you have many model parameters, this is less likely
You always find a way down in some direction
Models with many parameters typically find good local minima
Intuition: walking downhill using only the slope you “feel” nearby

(Image by A. Karpathy)
Stochastic Gradient Descent (SGD)#
Compute gradients not on the entire dataset, but on a single data point \(i\) at a time
Gradient descent: \(\mathbf{w}^{s+1} = \mathbf{w}^s-\eta\nabla \mathcal{L}(\mathbf{w}^s) = \mathbf{w}^s-\frac{\eta}{n} \sum_{i=1}^{n} \nabla \mathcal{L_i}(\mathbf{w}^s)\)
Stochastic Gradient Descent: \(\mathbf{w}^{s+1} = \mathbf{w}^s-\eta\nabla \mathcal{L_i}(\mathbf{w}^s)\)
Many smoother variants, e.g.
Minibatch SGD: compute gradient on batches of data: \(\mathbf{w}^{s+1} = \mathbf{w}^s-\frac{\eta}{B} \sum_{i=1}^{B} \nabla \mathcal{L_i}(\mathbf{w}^s)\)
Stochastic Average Gradient Descent (SAG). With \(i_s \in [1,n]\) randomly chosen per iteration:
Incremental gradient: \(\mathbf{w}^{s+1} = \mathbf{w}^s-\frac{\eta}{n} \sum_{i=1}^{n} v_i^s\) with \(v_i^s = \begin{cases}\nabla \mathcal{L_i}(\mathbf{w}^s) & i = i_s \\ v_i^{s-1} & \text{otherwise} \end{cases}\)
In practice#
Linear regression can be found in
sklearn.linear_model. We’ll evaluate it on the Boston Housing dataset.LinearRegressionuses closed form solution,SGDRegressorwithloss='squared_loss'uses Stochastic Gradient DescentLarge coefficients signal overfitting
Test score is much lower than training score
Show code cell source
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
X_B, y_B = mglearn.datasets.load_extended_boston()
X_B_train, X_B_test, y_B_train, y_B_test = train_test_split(X_B, y_B, random_state=0)
lr = LinearRegression().fit(X_B_train, y_B_train)
Show code cell source
print("Weights (coefficients): {}".format(lr.coef_[0:40]))
print("Bias (intercept): {}".format(lr.intercept_))
Weights (coefficients): [ -412.711 -52.243 -131.899 -12.004 -15.511 28.716 54.704
-49.535 26.582 37.062 -11.828 -18.058 -19.525 12.203
2980.781 1500.843 114.187 -16.97 40.961 -24.264 57.616
1278.121 -2239.869 222.825 -2.182 42.996 -13.398 -19.389
-2.575 -81.013 9.66 4.914 -0.812 -7.647 33.784
-11.446 68.508 -17.375 42.813 1.14 ]
Bias (intercept): 30.934563673643545
Show code cell source
print("Training set score (R^2): {:.2f}".format(lr.score(X_B_train, y_B_train)))
print("Test set score (R^2): {:.2f}".format(lr.score(X_B_test, y_B_test)))
Training set score (R^2): 0.95
Test set score (R^2): 0.61
Ridge regression#
Adds a penalty term to the least squares loss function:
Model is penalized if it uses large coefficients (\(w\))
Each feature should have as little effect on the outcome as possible
We don’t want to penalize \(w_0\), so we leave it out
Regularization: explicitly restrict a model to avoid overfitting.
Called L2 regularization because it uses the L2 norm: \(\sum w_i^2\)
The strength of the regularization can be controlled with the \(\alpha\) hyperparameter.
Increasing \(\alpha\) causes more regularization (or shrinkage). Default is 1.0.
Still convex. Can be optimized in different ways:
Closed form solution (a.k.a. Cholesky): \(w^{*} = (X^{T}X + \alpha I)^{-1} X^T \mathbf{y}\)
Gradient descent and variants, e.g. Stochastic Average Gradient (SAG,SAGA)
Conjugate gradient (CG): each new gradient is influenced by previous ones
Use Cholesky for smaller datasets, Gradient descent for larger ones
Ridge Regression Derivation#
We want to minimize the Ridge loss function with respect to \(\mathbf{w}\):
Expanding:
Taking the derivative with respect to \(\mathbf{w}\):
Setting the derivative equal to zero:
In practice#
from sklearn.linear_model import Ridge
lr = Ridge().fit(X_train, y_train)
Show code cell source
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_B_train, y_B_train)
print("Weights (coefficients): {}".format(ridge.coef_[0:40]))
print("Bias (intercept): {}".format(ridge.intercept_))
print("Training set score: {:.2f}".format(ridge.score(X_B_train, y_B_train)))
print("Test set score: {:.2f}".format(ridge.score(X_B_test, y_B_test)))
Weights (coefficients): [-1.414 -1.557 -1.465 -0.127 -0.079 8.332 0.255 -4.941 3.899 -1.059
-1.584 1.051 -4.012 0.334 0.004 -0.849 0.745 -1.431 -1.63 -1.405
-0.045 -1.746 -1.467 -1.332 -1.692 -0.506 2.622 -2.092 0.195 -0.275
5.113 -1.671 -0.098 0.634 -0.61 0.04 -1.277 -2.913 3.395 0.792]
Bias (intercept): 21.390525958610052
Training set score: 0.89
Test set score: 0.75
Test set score is higher and training set score lower: less overfitting!
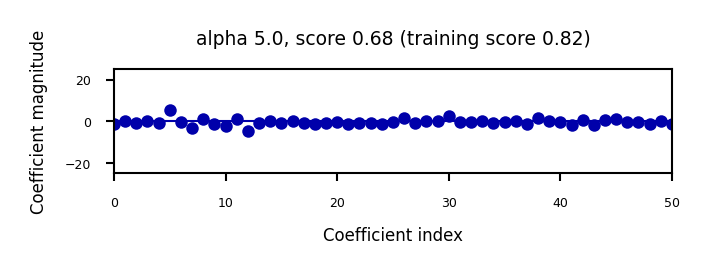
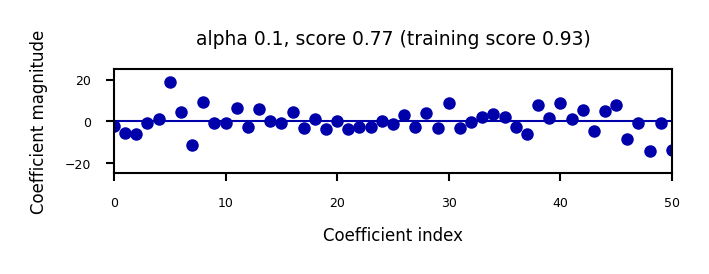
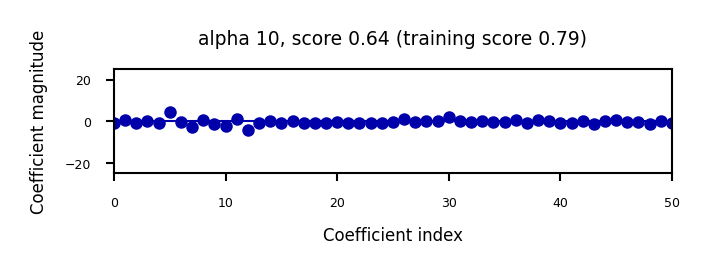
We can plot the weight values for differents levels of regularization to explore the effect of \(\alpha\).
Increasing regularization decreases the values of the coefficients, but never to 0.
Show code cell source
from __future__ import print_function
import ipywidgets as widgets
from ipywidgets import interact, interact_manual
from sklearn.linear_model import Ridge
@interact
def plot_ridge(alpha=(0,10.0,1)):
r = Ridge(alpha=alpha).fit(X_B_train, y_B_train)
fig, ax = plt.subplots(figsize=(8*fig_scale,1.5*fig_scale))
ax.plot(r.coef_, 'o', markersize=3)
ax.set_title("alpha {}, score {:.2f} (training score {:.2f})".format(alpha, r.score(X_B_test, y_B_test), r.score(X_B_train, y_B_train)))
ax.set_xlabel("Coefficient index")
ax.set_ylabel("Coefficient magnitude")
ax.hlines(0, 0, len(r.coef_))
ax.set_ylim(-25, 25)
ax.set_xlim(0, 50)
Show code cell output
Show code cell source
if not interactive:
for alpha in [0.1, 10]:
plot_ridge(alpha)
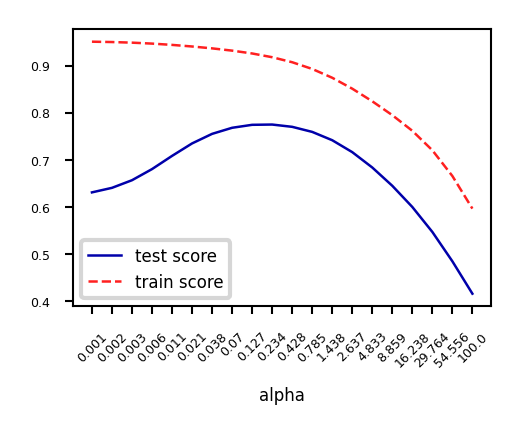
When we plot the train and test scores for every \(\alpha\) value, we see a sweet spot around \(\alpha=0.2\)
Models with smaller \(\alpha\) are overfitting
Models with larger \(\alpha\) are underfitting
Show code cell source
alpha=np.logspace(-3,2,num=20)
ai = list(range(len(alpha)))
test_score=[]
train_score=[]
for a in alpha:
r = Ridge(alpha=a).fit(X_B_train, y_B_train)
test_score.append(r.score(X_B_test, y_B_test))
train_score.append(r.score(X_B_train, y_B_train))
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
ax.set_xticks(range(20))
ax.set_xticklabels(np.round(alpha,3))
ax.set_xlabel('alpha')
ax.plot(test_score, lw=2*fig_scale, label='test score')
ax.plot(train_score, lw=2*fig_scale, label='train score')
ax.legend()
plt.xticks(rotation=45);
Other ways to reduce overfitting#
Add more training data: with enough training data, regularization becomes less important
Ridge and ordinary least squares will have the same performance
Use fewer features: remove unimportant ones or find a low-dimensional embedding (e.g. PCA)
Fewer coefficients to learn, reduces the flexibility of the model
Scaling the data typically helps (and changes the optimal \(\alpha\) value)
Show code cell source
fig, ax = plt.subplots(figsize=(10*fig_scale,4*fig_scale))
mglearn.plots.plot_ridge_n_samples(ax)

Lasso (Least Absolute Shrinkage and Selection Operator)#
Adds a different penalty term to the least squares sum:
Called L1 regularization because it uses the L1 norm
Will cause many weights to be exactly 0
Same parameter \(\alpha\) to control the strength of regularization.
Will again have a ‘sweet spot’ depending on the data
No closed-form solution
Convex, but no longer strictly convex, and not differentiable
Weights can be optimized using coordinate descent
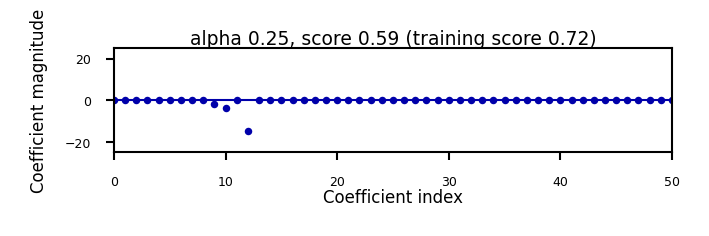
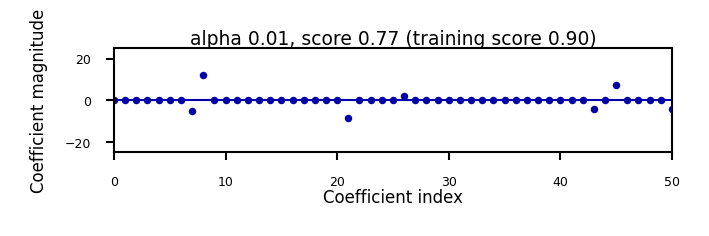
Analyze what happens to the weights:
L1 prefers coefficients to be exactly zero (sparse models)
Some features are ignored entirely: automatic feature selection
How can we explain this?
Show code cell source
from sklearn.linear_model import Lasso
@interact
def plot_lasso(alpha=(0,0.5,0.005)):
r = Lasso(alpha=alpha).fit(X_B_train, y_B_train)
fig, ax = plt.subplots(figsize=(8*fig_scale,1.5*fig_scale))
ax.plot(r.coef_, 'o', markersize=6*fig_scale)
ax.set_title("alpha {}, score {:.2f} (training score {:.2f})".format(alpha, r.score(X_B_test, y_B_test), r.score(X_B_train, y_B_train)), pad=0.5)
ax.set_xlabel("Coefficient index", labelpad=0)
ax.set_ylabel("Coefficient magnitude")
ax.hlines(0, 0, len(r.coef_))
ax.set_ylim(-25, 25);
ax.set_xlim(0, 50);
Show code cell output
Show code cell source
if not interactive:
for alpha in [0.00001, 0.01]:
plot_lasso(alpha)

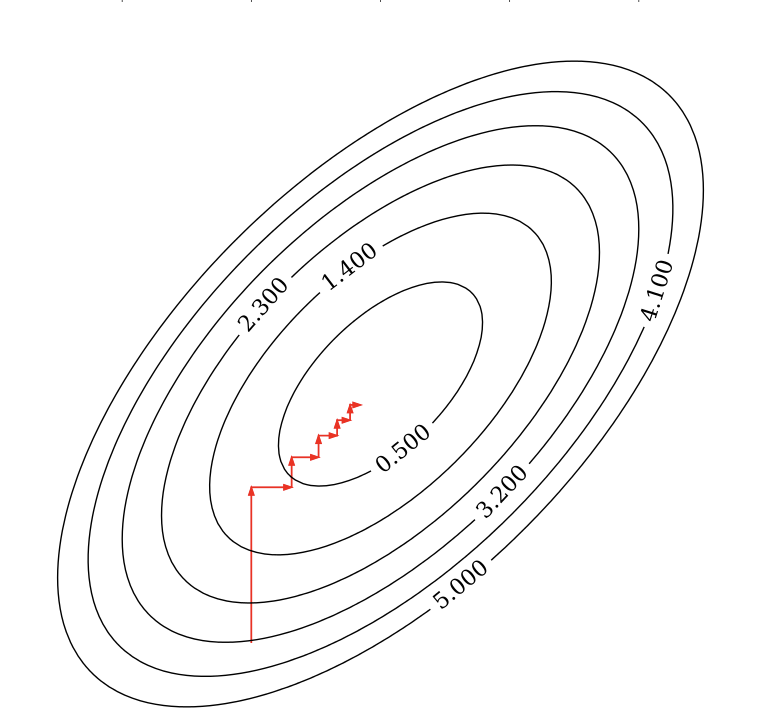
Coordinate descent#
Alternative for gradient descent, supports non-differentiable convex loss functions (e.g. \(\mathcal{L}_{Lasso}\))
In every iteration, optimize a single coordinate \(w_i\) (find minimum in direction of \(x_i\))
Continue with another coordinate, using a selection rule (e.g. round robin)
Faster iterations. No need to choose a step size (learning rate).
May converge more slowly. Can’t be parallellized.
Coordinate descent with Lasso (Further Reading)#
Remember that \(\mathcal{L}_{Lasso} = \mathcal{L}_{SSE} + \alpha \sum_{i=1}^{p} |w_i|\)
For one \(w_i\): \(\mathcal{L}_{Lasso}(w_i) = \mathcal{L}_{SSE}(w_i) + \alpha |w_i|\)
The L1 term is not differentiable but convex: we can compute the subgradient
Unique at points where \(\mathcal{L}\) is differentiable, a range of all possible slopes [a,b] where it is not
For \(|w_i|\), the subgradient \(\partial_{w_i} |w_i|\) = \(\begin{cases}-1 & w_i<0\\ [-1,1] & w_i=0 \\ 1 & w_i>0 \\ \end{cases}\)
Subdifferential \(\partial(f+g) = \partial f + \partial g\) if \(f\) and \(g\) are both convex
To find the optimum for Lasso \(w_i^{*}\), solve
\[\begin{split}\begin{aligned} \partial_{w_i} \mathcal{L}_{Lasso}(w_i) &= \partial_{w_i} \mathcal{L}_{SSE}(w_i) + \partial_{w_i} \alpha |w_i| \\ 0 &= (w_i - \rho_i) + \alpha \cdot \partial_{w_i} |w_i| \\ w_i &= \rho_i - \alpha \cdot \partial_{w_i} |w_i| \end{aligned}\end{split}\]In which \(\rho_i\) is the part of \(\partial_{w_i} \mathcal{L}_{SSE}(w_i)\) excluding \(w_i\) (assume \(z_i=1\) for now)
\(\rho_i\) can be seen as the \(\mathcal{L}_{SSE}\) ‘solution’: \(w_i = \rho_i\) if \(\partial_{w_i} \mathcal{L}_{SSE}(w_i) = 0\)
\[\partial_{w_i} \mathcal{L}_{SSE}(w_i) = \partial_{w_i} \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 = z_i w_i -\rho_i \]
We found: \(w_i = \rho_i - \alpha \cdot \partial_{w_i} |w_i|\)
The Lasso solution has the form of a soft thresholding function \(S\)
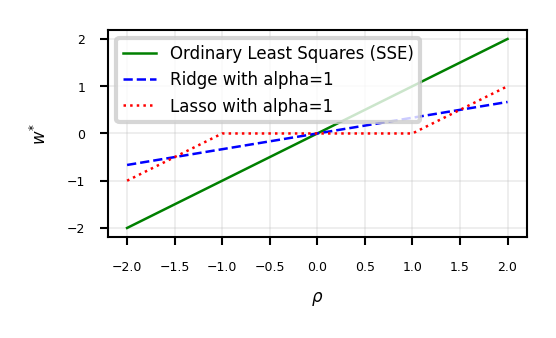
\[\begin{split}w_i^* = S(\rho_i,\alpha) = \begin{cases} \rho_i + \alpha, & \rho_i < -\alpha \\ 0, & -\alpha < \rho_i < \alpha \\ \rho_i - \alpha, & \rho_i > \alpha \\ \end{cases}\end{split}\]Small weights become 0: sparseness!
If the data is not normalized, \(w_i^* = \frac{1}{z_i}S(\rho_i,\alpha)\) with constant \(z_i = \sum_{n=1}^{N} x_{ni}^2\)
Ridge solution: \(w_i = \rho_i - \alpha \cdot \partial_{w_i} w_i^2 = \rho_i - 2\alpha \cdot w_i\), thus \(w_i^* = \frac{\rho_i}{1 + 2\alpha}\)
For mor information see [Ras16]
Show code cell content
@interact
def plot_rho(alpha=(0,2.0,0.05)):
w = np.linspace(-2,2,101)
r = w/(1+2*alpha)
l = [x+alpha if x <= -alpha else (x-alpha if x > alpha else 0) for x in w]
fig, ax = plt.subplots(figsize=(6*fig_scale,3*fig_scale))
ax.set_xlabel(r'$\rho$')
ax.set_ylabel(r'$w^{*}$')
ax.plot(w, w, lw=2*fig_scale, c='g', label='Ordinary Least Squares (SSE)')
ax.plot(w, r, lw=2*fig_scale, c='b', label='Ridge with alpha={}'.format(alpha))
ax.plot(w, l, lw=2*fig_scale, c='r', label='Lasso with alpha={}'.format(alpha))
ax.legend()
plt.grid()

Show code cell content
if not interactive:
plot_rho(alpha=1)
Interpreting L1 and L2 loss#
Show code cell content
def c_fx(x):
fX = ((x * 2 - 1)**2) # Some convex function to represent the loss
return fX/9 # Scaling
def c_fl2(x,alpha):
return c_fx(x) + alpha * x**2
def c_fl1(x,alpha):
return c_fx(x) + alpha * abs(x)
def l2(x,alpha):
return alpha * x**2
def l1(x,alpha):
return alpha * abs(x)
@interact
def plot_losses(alpha=(0,1.0,0.05)):
w = np.linspace(-1,1,101)
f = [c_fx(i) for i in w]
r = [c_fl2(i,alpha) for i in w]
l = [c_fl1(i,alpha) for i in w]
rp = [l2(i,alpha) for i in w]
lp = [l1(i,alpha) for i in w]
fig, ax = plt.subplots(figsize=(8*fig_scale,4*fig_scale))
ax.set_xlabel('w')
ax.set_ylabel('loss')
ax.plot(w, rp, lw=1.5*fig_scale, ls=':', c='b', label='L2 with alpha={}'.format(alpha))
ax.plot(w, lp, lw=1.5*fig_scale, ls=':', c='r', label='L1 with alpha={}'.format(alpha))
ax.plot(w, f, lw=2*fig_scale, ls='-', c='k', label='Least Squares loss')
ax.plot(w, r, lw=2*fig_scale, ls='-', c='b', label='Loss + L2 (Ridge)'.format(alpha))
ax.plot(w, l, lw=2*fig_scale, ls='-', c='r', label='Loss + L1 (Lasso)'.format(alpha))
opt_f = np.argmin(f)
ax.scatter(w[opt_f], f[opt_f], c="k", s=50*fig_scale)
opt_r = np.argmin(r)
ax.scatter(w[opt_r], r[opt_r], c="b", s=50*fig_scale)
opt_l = np.argmin(l)
ax.scatter(w[opt_l], l[opt_l], c="r", s=50*fig_scale)
ax.legend()
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.ylim(-0.1,1)
plt.grid()

Show code cell content
if not interactive:
plot_losses(alpha=0.5)

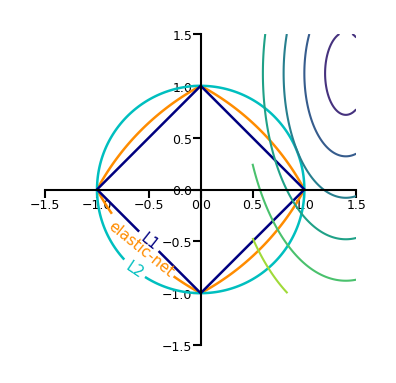
In 2D (for 2 model weights \(w_1\) and \(w_2\))
The least squared loss is a 2D convex function in this space
For illustration, assume that L1 loss = L2 loss = 1
L1 loss (\(\Sigma |w_i|\)): every {\(w_1, w_2\)} falls on the diamond
L2 loss (\(\Sigma w_i^2\)): every {\(w_1, w_2\)} falls on the circle
For L1, the loss is minimized if \(w_1\) or \(w_2\) is 0 (rarely so for L2)
Show code cell source
def plot_loss_interpretation():
line = np.linspace(-1.5, 1.5, 1001)
xx, yy = np.meshgrid(line, line)
l2 = xx ** 2 + yy ** 2
l1 = np.abs(xx) + np.abs(yy)
rho = 0.7
elastic_net = rho * l1 + (1 - rho) * l2
plt.figure(figsize=(5*fig_scale, 4*fig_scale))
ax = plt.gca()
elastic_net_contour = plt.contour(xx, yy, elastic_net, levels=[1], linewidths=2*fig_scale, colors="darkorange")
l2_contour = plt.contour(xx, yy, l2, levels=[1], linewidths=2*fig_scale, colors="c")
l1_contour = plt.contour(xx, yy, l1, levels=[1], linewidths=2*fig_scale, colors="navy")
ax.set_aspect("equal")
ax.spines['left'].set_position('center')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('center')
ax.spines['top'].set_color('none')
plt.clabel(elastic_net_contour, inline=1, fontsize=12*fig_scale,
fmt={1.0: 'elastic-net'}, manual=[(-0.6, -0.6)])
plt.clabel(l2_contour, inline=1, fontsize=12*fig_scale,
fmt={1.0: 'L2'}, manual=[(-0.5, -0.5)])
plt.clabel(l1_contour, inline=1, fontsize=12*fig_scale,
fmt={1.0: 'L1'}, manual=[(-0.5, -0.5)])
x1 = np.linspace(0.5, 1.5, 100)
x2 = np.linspace(-1.0, 1.5, 100)
X1, X2 = np.meshgrid(x1, x2)
y = np.sqrt(np.square(X1/2-0.7) + np.square(X2/4-0.28))
cp = plt.contour(X1, X2, y)
#plt.clabel(cp, inline=1, fontsize=10)
ax.tick_params(axis='both', pad=0)
plt.tight_layout()
plt.show()
plot_loss_interpretation()
Comparing Ridge and LASSO for Prediction and Feature Selection#
The following code trains and compares Linear Regression, Ridge (L2), and LASSO (L1) regression models. We’ll examine their predictive performance using Mean Squared Error (MSE) and observe how LASSO can be used for feature selection by shrinking some feature coefficients to zero.
Show code cell source
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, Lasso, LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
import mglearn
import warnings
from sklearn.exceptions import InconsistentVersionWarning # More specific if available, or use UserWarning
# Suppress the specific UserWarning from _openml.py
warnings.filterwarnings("ignore", category=UserWarning, module="sklearn.datasets._openml")
# Load extended Boston dataset (with polynomial features)
X_B, y_B = mglearn.datasets.load_extended_boston()
X_B_train, X_B_test, y_B_train, y_B_test = train_test_split(X_B, y_B, random_state=0)
# Train models
lr = LinearRegression().fit(X_B_train, y_B_train)
ridge = Ridge(alpha=0.2).fit(X_B_train, y_B_train)
lasso = Lasso(alpha=0.01, max_iter=5000).fit(X_B_train, y_B_train) # Increased max_iter for convergence
# Compare errors
print("Linear Regression MSE:", mean_squared_error(y_B_test, lr.predict(X_B_test)))
print("Ridge MSE:", mean_squared_error(y_B_test, ridge.predict(X_B_test)))
print("LASSO MSE:", mean_squared_error(y_B_test, lasso.predict(X_B_test)))
# Feature selection with LASSO (non-zero coefficients)
feature_names = [f"Feature {i}" for i in range(X_B.shape[1])]
lasso_coef = pd.Series(lasso.coef_, index=feature_names)
lasso_nnz = len(lasso_coef[lasso_coef != 0])
print(f"\nLASSO selected {lasso_nnz} features from total {len(lasso_coef)} features.")
Linear Regression MSE: 32.06913512158206
Ridge MSE: 18.386795859109146
LASSO MSE: 19.145582778836758
LASSO selected 33 features from total 104 features.
Elastic-Net#
Adds both L1 and L2 regularization:
\(\rho\) is the L1 ratio
With \(\rho=1\), \(\mathcal{L}_{Elastic} = \mathcal{L}_{Lasso}\)
With \(\rho=0\), \(\mathcal{L}_{Elastic} = \mathcal{L}_{Ridge}\)
\(0 < \rho < 1\) sets a trade-off between L1 and L2.
Allows learning sparse models (like Lasso) while maintaining L2 regularization benefits
E.g. if 2 features are correlated, Lasso likely picks one randomly, Elastic-Net keeps both
Weights can be optimized using coordinate descent (similar to Lasso)
Sparse Optimization: Theory and Applications#
Sparse optimization is a fundamental paradigm in mathematical modeling that seeks solutions with few non-zero elements, often formalized through ℓ₁-norm regularization or non-convex penalties. This framework is grounded in the Compressed Sensing (CS) theory [Don06], which guarantees exact signal recovery from sub-Nyquist measurements if the signal is sparse in some basis. Key applications include:
Medical Imaging: CS enables faster MRI scans by reconstructing images from limited k-space samples (Lustig et al., 2007), as highlighted in the CUHK lecture notes on CS (p. 13).
Signal Processing: Sparse methods underpin denoising (e.g., wavelet shrinkage) and inpainting, where total variation minimization preserves edges while removing noise (Figueiredo, 2021, slides p. 8).
Machine Learning: Sparse regression (e.g., LASSO; Tibshirani, 1996) and robust PCA (Candès et al., 2011) are critical for feature selection and anomaly detection. The Ghent tutorial (p. 5) further links sparsity to deep network pruning.
Statistics: High-dimensional inference (e.g., genomics) benefits from sparsity-induced interpretability (Bühlmann & Van de Geer, 2011).
The field continues to evolve with non-convex penalties (e.g., SCAD) and greedy algorithms (OMP), balancing computational efficiency and statistical guarantees. For a unified perspective, see the cited references and tutorials.
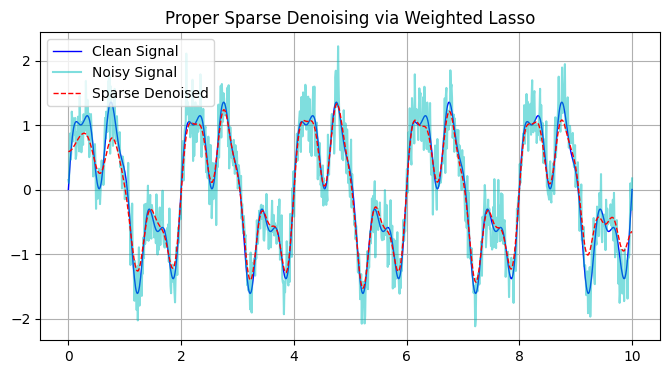
Sparse Signal Denoising via Weighted Lasso in DCT Domain#
Given a noisy 1D signal:
where:
f(t)is the clean signal (sparse in frequency domain)ϵ(t)is Gaussian noise (non-sparse in any basis)
We solve the weighted Lasso problem:
Noise-Sparsity Dichotomy#
Signal: Sparse in DCT domain (few dominant coefficients)
Noise: Non-sparse (energy spread across all frequencies)
Weighted ℓ₁ Magic#
Preserves signal structure (low frequencies)
Aggressively truncates noise (high frequencies)
Performance Analysis#
Theoretical Guarantees#
Exact Recovery: Possible if:
Signal truly sparse in DCT basis
Noise level below threshold (Donoho et al., 2006)
Stability: Weighted Lasso provides better coefficient preservation than standard Lasso
Limitations#
Assumes signal sparsity in chosen basis
Requires tuning for each application
Computationally heavier than simple filtering
Signal Denoising using LASSO
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import dct, idct
from sklearn.linear_model import Lasso
# Generate clean signal with multiple frequencies
np.random.seed(42)
t = np.linspace(0, 10, 1000)
f_clean = (np.sin(2*np.pi*0.5*t) +
0.7*np.sin(2*np.pi*1.5*t - 0.2) +
0.3*np.sin(2*np.pi*3*t + 0.5))
# Add noise
noise = 0.3 * np.random.randn(len(t))
f_noisy = f_clean + noise
def sparse_denoise(signal, alpha=0.05):
"""Denoise using Lasso in DCT domain with proper frequency retention"""
# DCT transform (sparse representation)
dct_coeffs = dct(signal, norm='ortho')
model = Lasso(alpha=alpha,
max_iter=10000,
warm_start=True,
selection='random')
model.coef_ = dct_coeffs # Initialize with DCT coeffs
# Solve ||y - DCT^-1(x)||² + alpha * ||x||₁
X = np.eye(len(signal))
model.fit(X, dct_coeffs)
# Count total number of coefficients
total_coefs = model.coef_.shape[0]
# Count number of non-zero coefficients (NNZ)
nnz_count = np.count_nonzero(model.coef_)
print(f"Total number of coefficients: {total_coefs}")
print(f"Number of non-zero coefficients (NNZ): {nnz_count}")
return idct(model.coef_, norm='ortho')
# Denoise with proper parameters
f_denoised = sparse_denoise(f_noisy, alpha=0.0009)
# Plot
plt.figure(figsize=(8, 4))
plt.plot(t, f_clean, 'b-', lw=1, label='Clean Signal')
plt.plot(t, f_noisy, 'c-', alpha=0.5, label='Noisy Signal')
plt.plot(t, f_denoised, 'r--', lw=1, label='Sparse Denoised')
plt.legend()
plt.title('Proper Sparse Denoising via Weighted Lasso')
plt.grid(True)
plt.show()
Total number of coefficients: 1000
Number of non-zero coefficients (NNZ): 25
Orthogonal Matching Pursuit (OMP) for Sparse Recovery#
Orthogonal Matching Pursuit (OMP) is a greedy algorithm that solves the sparse approximation problem:
Problem Statement: Given a design matrix \(X \in \mathbb{R}^{n \times p}\) (where typically \(n \ll p\)) and observations \(\mathbf{y} \in \mathbb{R}^n\), find the sparsest vector \(\mathbf{w} \in \mathbb{R}^p\) such that \(\mathbf{y} \approx X\mathbf{w}\).
Key characteristics:
Iterative approach that selects one feature per iteration based on maximum correlation
Provides exact recovery guarantees under Restricted Isometry Property (RIP) conditions
Computationally efficient (\(O(knp)\) complexity) compared to \(\ell_0\)-norm minimization
Widely used in compressed sensing, signal processing, and feature selection
Preserves interpretability through explicit feature selection
This method complements LASSO by offering an alternative approach to sparse recovery with distinct theoretical guarantees and computational trade-offs.
While LASSO solves the \(\ell_1\)-regularized problem:
OMP provides a greedy alternative for sparse approximation, solving:
OMP algorithm#
Given:
Design matrix \(X \in \mathbb{R}^{n \times p}\)
Response vector \(\mathbf{y} \in \mathbb{R}^n\)
Target sparsity level \(k\)
At each iteration:
Select most correlated feature: \(j = \arg\max_{j \notin \mathcal{A}} |\mathbf{x}_j^\top \mathbf{r}|\), where \(\mathbf{r}\) is the current residual and \(\mathcal{A}\) is the active feature set.
Update support: \(\mathcal{A} \leftarrow \mathcal{A} \cup \{j\}\)
Solve least squares: \(\mathbf{w} = \arg\min_{\mathbf{w}} \|X_{\mathcal{A}}\mathbf{w} - \mathbf{y}\|_2^2\)
Update residual: \(\mathbf{r} \leftarrow X_{\mathcal{A}}\mathbf{w} - \mathbf{y}\)
Termination: After \(k\) iterations or when \(\|\mathbf{r}\|_2 < \epsilon\)
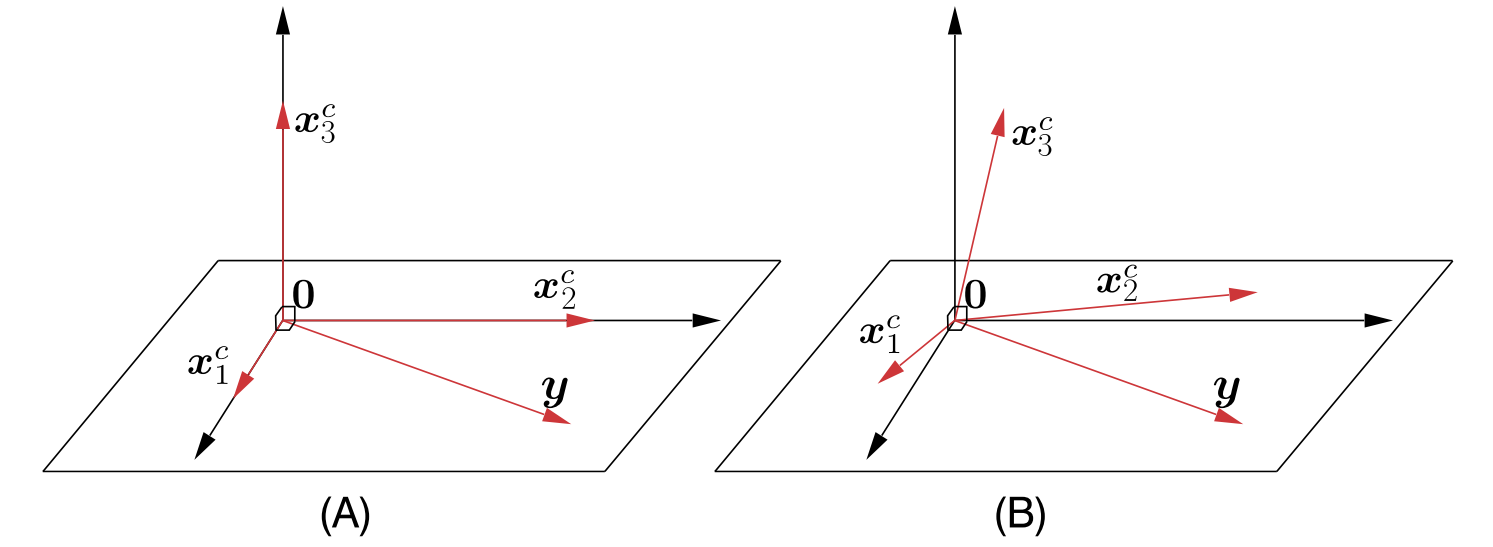
Figure 10.2 of [The20]:
(A) In the case of an orthogonal matrix, the observations vector y will be orthogonal to any inactive column, here, \(x_3^c\). (B) In the more general case, it is expected to “lean” closer (form smaller angles) to the active than to the inactive columns.

Figure 2.3 of [Bak18]
Comparison with LASSO#
Property |
OMP |
LASSO |
|---|---|---|
Objective |
\(\ell_0\) constraint |
\(\ell_1\) regularization |
Solution |
Greedy approximation |
Convex optimization |
Computational |
Faster for small \(k\) |
Slower but more stable |
Theoretical |
Exact recovery possible |
Consistent estimation |
For further information see [Asa16].
Practice#
import numpy as np
from numpy.linalg import pinv
def omp(X, y, k, tol=1e-6):
"""
Orthogonal Matching Pursuit
Parameters
----------
X : ndarray, shape (n_samples, n_features)
Design matrix
y : ndarray, shape (n_samples,)
Target vector
k : int
Sparsity level (number of non-zero coefficients)
tol : float
Residual tolerance for early stopping
Returns
-------
w : ndarray, shape (n_features,)
Sparse coefficient vector
"""
n, p = X.shape
w = np.zeros(p)
residual = y.copy()
active = []
for _ in range(k):
# Find most correlated feature
correlations = np.abs(X.T @ residual)
correlations[active] = -np.inf # exclude selected
new_idx = np.argmax(correlations)
active.append(new_idx)
# Solve least squares on active set
X_active = X[:, active]
w_active = pinv(X_active) @ y
# Update residual
residual = y - X_active @ w_active
# Early stopping if residual is small
if np.linalg.norm(residual) < tol:
break
# Convert to full coefficient vector
w_sparse = np.zeros(p)
w_sparse[active] = w_active
return w_sparse
Show code cell source
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
# Generate synthetic data
np.random.seed(42)
n, p = 100, 200
X = np.random.randn(n, p)
w_true = np.zeros(p)
w_true[[5, 45, 100]] = [1.5, -0.8, 1.2]
y = X @ w_true + 0.1 * np.random.randn(n)
# Split into train/test (80/20)
split_idx = int(0.8 * n)
X_train, X_test = X[:split_idx], X[split_idx:]
y_train, y_test = y[:split_idx], y[split_idx:]
# --- Run OMP ---
w_omp = omp(X_train, y_train, k=3)
# --- Run LASSO ---
lasso = Lasso(alpha=0.1).fit(X_train, y_train)
w_lasso = lasso.coef_
# --- Evaluation Metrics ---
# Print ground truth for reference
true_nnz = w_true[w_true != 0]
print("\nGround Truth Non-zero Coefficients:", ", ".join([f"{val:.2f}" for val in true_nnz]))
print("\nPerformance Comparison:")
print(f"{'Method':<10} {'Test MSE':<12} {'Support Error':<15} {'ℓ2 Error':<10} {'Non-zero Coefficients':<30}")
print("-"*75)
for name, w in [('OMP', w_omp), ('LASSO', w_lasso)]:
test_mse = np.mean((X_test @ w - y_test)**2)
support_error = np.sum((w != 0) != (w_true != 0))
l2_error = np.linalg.norm(w - w_true)
nnz_values = w[w != 0]
# Format NNZ values with 2 decimal places
nnz_str = ", ".join([f"{val:.2f}" for val in nnz_values[:5]]) # Show first 5
if len(nnz_values) > 5:
nnz_str += ", ..."
print(f"{name:<10} {test_mse:.4e} {support_error:<15} {l2_error:<10.4f} [{nnz_str}]")
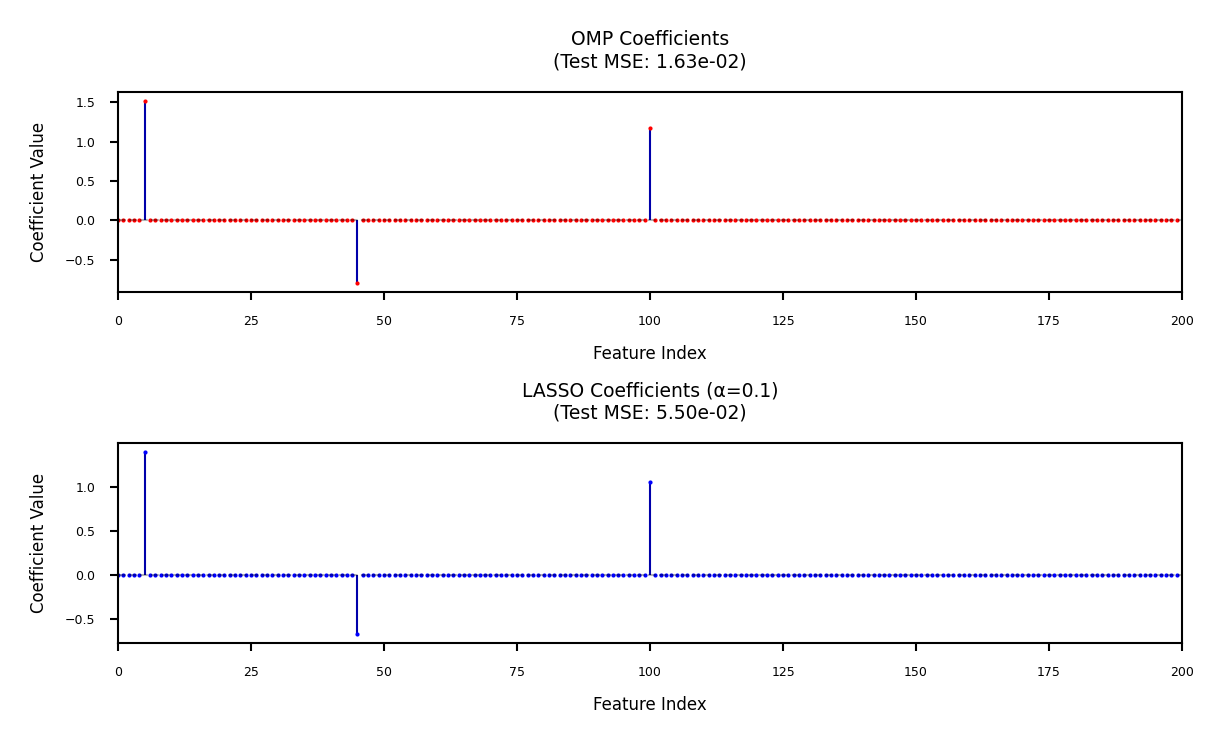
Ground Truth Non-zero Coefficients: 1.50, -0.80, 1.20
Performance Comparison:
Method Test MSE Support Error ℓ2 Error Non-zero Coefficients
---------------------------------------------------------------------------
OMP 1.6293e-02 0 0.0296 [1.51, -0.80, 1.17]
LASSO 5.5046e-02 0 0.2214 [1.39, -0.68, 1.05]
Show code cell content
# --- Coefficient Visualization ---
plt.figure(figsize=(4, 8*fig_scale))
# OMP Plot
plt.subplot(2, 1, 1)
plt.stem(w_omp, markerfmt='ro', basefmt=" ")
plt.title(f"OMP Coefficients\n(Test MSE: {np.mean((X_test @ w_omp - y_test)**2):.2e})")
plt.xlabel("Feature Index")
plt.ylabel("Coefficient Value")
plt.axhline(0, color='k', linestyle='--', alpha=0.3)
plt.xlim(0, p)
# LASSO Plot
plt.subplot(2, 1, 2)
plt.stem(w_lasso, markerfmt='bo', basefmt=" ")
plt.title(f"LASSO Coefficients (α=0.1)\n(Test MSE: {np.mean((X_test @ w_lasso - y_test)**2):.2e})")
plt.xlabel("Feature Index")
plt.ylabel("Coefficient Value")
plt.axhline(0, color='k', linestyle='--', alpha=0.3)
plt.xlim(0, p)
plt.tight_layout()
plt.show()
When to Use OMP#
Exactly sparse signals – OMP is ideal when the underlying signal truly has only a few non-zero coefficients, making it a strong choice for enforcing strict sparsity.
Small-scale problems – Works efficiently when the number of non-zero elements \( k \) is much smaller than the total features \( p \) (i.e., \( k \ll p \)), preventing unnecessary computational overhead.
Interpretable solutions – Since OMP selects features iteratively, the stepwise approach makes it easier to analyze which features contribute to the model, often simpler than interpreting LASSO’s continuous shrinkage.
Dictionary learning – Frequently used in sparse coding applications, where signals are represented as a sparse combination of dictionary elements, making it valuable for feature selection in compressed sensing.
Connection Between Sparse Learning and Functional Analysis#
Sparse recovery techniques like OMP and LASSO are deeply rooted in functional analysis, which explains why terms like Hilbert spaces and Banach spaces frequently appear in machine learning research. These mathematical frameworks provide the theoretical foundation for understanding sparsity-inducing methods.
Hilbert Spaces and Orthogonal Projections#
Hilbert spaces (complete inner product spaces) are essential for analyzing orthogonal projections and basis expansions. For example:
OMP iteratively projects the residual onto the span of selected basis vectors, leveraging the orthogonality principle to minimize error at each step.
The inner product structure of Hilbert spaces enables efficient computation of correlations between residuals and dictionary atoms (columns of \( X \)).
Banach Spaces and \( \ell_1 \)-Regularization#
LASSO operates in the context of Banach spaces (complete normed vector spaces) due to its reliance on the \( \ell_1 \)-norm:
The \( \ell_1 \)-norm’s non-smoothness at the origin induces sparsity, a property studied in Banach space geometry.
Unlike Hilbert spaces, Banach spaces generalize optimization techniques to non-Euclidean settings, crucial for sparse regularization.
Fourier, Wavelet, and Other Representations#
Sparse learning often exploits transform domains (e.g., Fourier, wavelet, or learned dictionaries) where signals admit concise representations: - These domains provide structured bases where only a few coefficients are significant. - The connection to functional analysis arises because such bases typically form frames or Riesz bases in Hilbert spaces, ensuring stable sparse approximations.
From Fixed Bases to Learned Representations#
Classical Sparse Coding:
Relies on predefined bases (e.g., Fourier, wavelets) where signals admit sparse representations.
These bases often form frames or Riesz bases in Hilbert spaces, ensuring stable approximations.
Convolutional Neural Networks (CNNs):
Learn adaptive bases/filters from data, implicitly constructing sparse-like representations through:
Local connectivity: Filters act as localized basis functions.
Activation sparsity: ReLU promotes de facto sparsity in feature maps.
While CNNs lack explicit \( \ell_0 \)/\( \ell_1 \) constraints, their hierarchical structure approximates multi-scale sparse decompositions, akin to wavelet analysis but data-driven.
The Evolving Role of Sparse Methods#
While deep learning has reduced reliance on handcrafted sparse models in some domains, sparse methods remain relevant because:
Interpretability:
OMP/LASSO yield explicit basis selections, whereas CNNs operate as black boxes.
Critical in fields like medicine or physics where model transparency is required.
Data-Efficiency:
Sparse methods often outperform DL in low-data regimes (e.g., medical imaging with small datasets).
Theoretical Guarantees:
Compressed sensing (OMP) and convex optimization (LASSO) provide recovery guarantees under precise conditions, unlike empirical DL results.
Hybrid Approaches:
Modern architectures (e.g., ISTA-Net, Learned Iterative Shrinkage) blend sparse priors with deep learning, showing that sparsity remains a useful inductive bias.
Sparse learning and deep learning are complementary:
CNNs dominate when data is abundant and interpretability is secondary.
OMP/LASSO persist in scenarios requiring rigor, efficiency, or transparency.
Functional analysis bridges these paradigms, providing tools to analyze both fixed and learned representations.
MRI reconstruction (Further Reading)#
MRI reconstruction can be formulated as an inverse problem where the goal is to recover the original image \( \mathbf{m} \) from under-sampled k-space measurements \( \mathbf{y} \). This is achieved using sparse optimization techniques.
A common formulation for MRI reconstruction is:
where:
\( \mathbf{m} \) represents the MRI image to be reconstructed.
\( \mathbf{F}_u \) is the under-sampled Fourier operator, mapping the image to k-space.
\( \mathbf{y} \) is the acquired k-space data (limited measurements).
\( \Psi \) is the sparsifying transform (e.g., wavelet or total variation).
\( \|\Psi \mathbf{m}\|_p \) represents the sparsity constraint, often chosen as \( \ell_1 \) (similar to LASSO) or \( \ell_0 \) (similar to OMP).
\( \lambda \) controls the balance between data fidelity and sparsity enforcement.
By leveraging sparsity, MRI reconstruction enables faster scans with fewer measurements while preserving essential anatomical details.
PyTomography#
PyTomography is an open-source Python library designed for medical image reconstruction, particularly in SPECT (Single-Photon Emission Computed Tomography) and PET (Positron Emission Tomography) imaging. Developed to address the challenges of quantitative tomographic reconstruction, PyTomography provides a flexible, modular framework for implementing advanced reconstruction algorithms, including attenuation correction, scatter correction, and resolution modeling.
Key Features#
✅ Open-source & community-driven (GitHub)
✅ Supports multiple reconstruction techniques (OSEM, MLEM, deep learning-based methods)
✅ Integrates with GPU acceleration for faster computations
✅ Well-documented with tutorials and API references (ReadTheDocs)
✅ Validated in peer-reviewed research (Scientific Reports, 2024)
Why Use PyTomography?#
PyTomography bridges the gap between research and clinical applications by offering:
Reproducible reconstruction workflows
Customizable forward and backward projection models
Seamless integration with Python’s scientific computing stack (NumPy, PyTorch)
Whether for academic research, algorithm development, or clinical prototyping, PyTomography provides a powerful, accessible toolkit for next-generation medical imaging reconstruction.
PySAP#
The Python Sparse data Analysis Package (PySAP) was developed as part of COSMIC, a multi-disciplinary collaboration between NeuroSpin, experts in biomedical imaging, and CosmoStat, experts in astrophysical image processing. PySAP is designed to provide state-of-the-art signal processing tools for various imaging domains, including:
Astronomy
Electron Tomography
Magnetic Resonance Imaging (MRI)
One of PySAP’s core contributions lies in sparse optimization, a powerful technique widely used for reconstructing images from incomplete or noisy data. The package implements advanced compressed sensing algorithms[The20], allowing efficient image restoration while preserving essential features.
In medical imaging, PySAP plays a crucial role in MRI reconstruction by leveraging sparsity-based approaches to improve scan efficiency. It enables:
Reduced scanning time while maintaining image quality
Improved reconstruction of under-sampled k-space data
Integration of machine learning techniques for further enhancement
The first release of PySAP was presented in Farrens et al. [GGRR+20] and continues to evolve as a robust tool for sparse signal processing.
For further exploration, visit the PySAP GitHub repository.
In our deep learning course, we will encounter additional examples of minimizing \( ||Ax - b|| \), including applications like image deblurring and super-resolution.

For valuable references on Ridge and Shrinkage methods, consider consulting Prof. Arashi’s books [SAK19, SASN22].
Linear models for Classification#
Aims to find a hyperplane that separates the examples of each class.
For binary classification (2 classes), we aim to fit the following function:
\(\hat{y} = w_1 * x_1 + w_2 * x_2 +... + w_p * x_p + w_0 > 0\)
When \(\hat{y}<0\), predict class -1, otherwise predict class +1
Show code cell source
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
Xf, yf = mglearn.datasets.make_forge()
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
clf = LogisticRegression().fit(Xf, yf)
mglearn.tools.plot_2d_separator(clf, Xf,
ax=ax, alpha=.7, cm=mglearn.cm2)
mglearn.discrete_scatter(Xf[:, 0], Xf[:, 1], yf, ax=ax, s=10*fig_scale)
ax.set_title("Logistic Regression")
ax.set_xlabel("Feature 1")
ax.set_ylabel("Feature 2")
ax.legend(['Class -1','Class 1']);

There are many algorithms for linear classification, differing in loss function, regularization techniques, and optimization method
Most common techniques:
Convert target classes {neg,pos} to {0,1} and treat as a regression task
Logistic regression (Log loss)
Ridge Classification (Least Squares + L2 loss)
Find hyperplane that maximizes the margin between classes
Linear Support Vector Machines (Hinge loss)
Neural networks without activation functions
Perceptron (Perceptron loss)
SGDClassifier: can act like any of these by choosing loss function
Hinge, Log, Modified_huber, Squared_hinge, Perceptron
Logistic regression#
Aims to predict the probability that a point belongs to the positive class
Converts target values {negative (blue), positive (red)} to {0,1}
Fits a logistic (or sigmoid or S curve) function through these points
Maps (-Inf,Inf) to a probability [0,1]
\[ \hat{y} = \textrm{logistic}(f_{\theta}(\mathbf{x})) = \frac{1}{1+e^{-f_{\theta}(\mathbf{x})}} \]E.g. in 1D: \( \textrm{logistic}(x_1w_1+w_0) = \frac{1}{1+e^{-x_1w_1-w_0}} \)
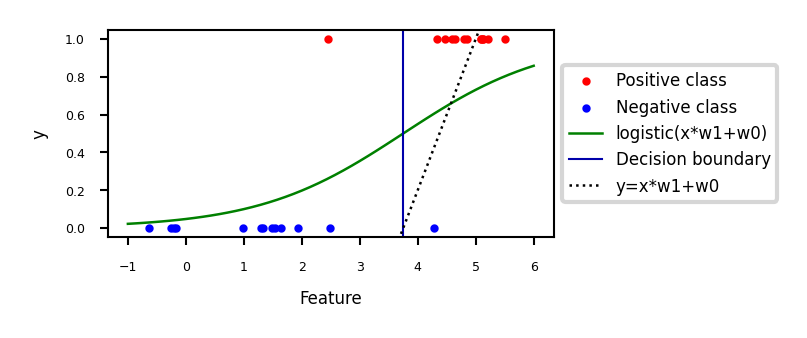
Show code cell source
def sigmoid(x,w1,w0):
return 1 / (1 + np.exp(-(x*w1+w0)))
@interact
def plot_logreg(w0=(-10.0,5.0,1),w1=(-1.0,3.0,0.3)):
fig, ax = plt.subplots(figsize=(8*fig_scale,3*fig_scale))
red = [Xf[i, 1] for i in range(len(yf)) if yf[i]==1]
blue = [Xf[i, 1] for i in range(len(yf)) if yf[i]==0]
ax.scatter(red, [1]*len(red), c='r', label='Positive class')
ax.scatter(blue, [0]*len(blue), c='b', label='Negative class')
x = np.linspace(min(-1, -w0/w1),max(6, -w0/w1))
ax.plot(x,sigmoid(x,w1,w0),lw=2*fig_scale,c='g', label='logistic(x*w1+w0)'.format(np.round(w0,2),np.round(w1,2)))
ax.axvline(x=(-w0/w1), ymin=0, ymax=1, label='Decision boundary')
ax.plot(x,x*w1+w0,lw=2*fig_scale,c='k',linestyle=':', label='y=x*w1+w0')
ax.set_xlabel("Feature")
ax.set_ylabel("y")
ax.set_ylim(-0.05,1.05)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height]);
Show code cell output
Show code cell source
if not interactive:
# fitted solution
clf2 = LogisticRegression(C=100).fit(Xf[:, 1].reshape(-1, 1), yf)
w0 = clf2.intercept_
w1 = clf2.coef_[0][0]
plot_logreg(w0=w0,w1=w1)
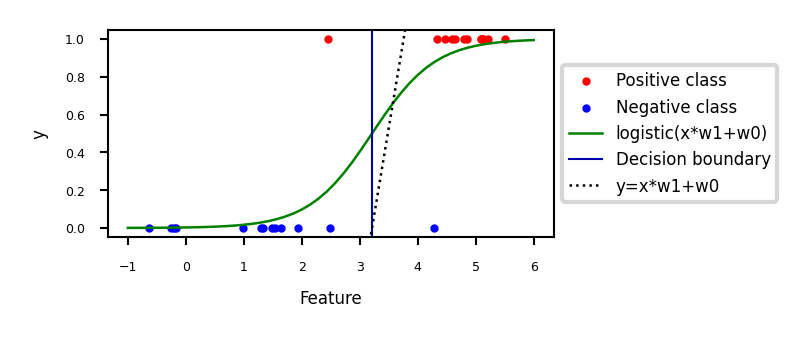
Fitted solution to our 2D example:
To get a binary prediction, choose a probability threshold (e.g. 0.5)
Show code cell source
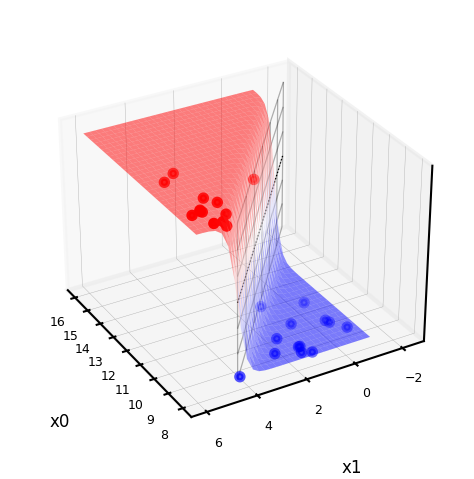
lr_clf = LogisticRegression(C=100).fit(Xf, yf)
def sigmoid2d(x1,x2,w0,w1,w2):
return 1 / (1 + np.exp(-(x2*w2+x1*w1+w0)))
@interact
def plot_logistic_fit(rotation=(0,360,10)):
w0 = lr_clf.intercept_
w1 = lr_clf.coef_[0][0]
w2 = lr_clf.coef_[0][1]
# plot surface of f
fig = plt.figure(figsize=(7*fig_scale,5*fig_scale))
ax = plt.axes(projection="3d")
x0 = np.linspace(8, 16, 30)
x1 = np.linspace(-1, 6, 30)
X0, X1 = np.meshgrid(x0, x1)
# Surface
ax.plot_surface(X0, X1, sigmoid2d(X0, X1, w0, w1, w2), rstride=1, cstride=1,
cmap='bwr', edgecolor='none',alpha=0.5,label='sigmoid')
# Points
c=['b','r']
ax.scatter3D(Xf[:, 0], Xf[:, 1], yf, c=[c[i] for i in yf], s=10*fig_scale)
# Decision boundary
# x2 = -(x1*w1 + w0)/w2
ax.plot3D(x0,-(x0*w1 + w0)/w2,[0.5]*len(x0), lw=1*fig_scale, c='k', linestyle=':')
z = np.linspace(0, 1, 31)
XZ, Z = np.meshgrid(x0, z)
YZ = -(XZ*w1 + w0)/w2
ax.plot_wireframe(XZ, YZ, Z, rstride=5, lw=1*fig_scale, cstride=5, alpha=0.3, color='k',label='decision boundary')
ax.tick_params(axis='both', width=0, labelsize=10*fig_scale, pad=-4)
ax.set_xlabel('x0', labelpad=-6)
ax.set_ylabel('x1', labelpad=-6)
ax.get_zaxis().set_ticks([])
ax.view_init(30, rotation) # Use this to rotate the figure
plt.tight_layout()
#plt.legend() # Doesn't work yet, bug in matplotlib
plt.show()
Show code cell source
if not interactive:
plot_logistic_fit(rotation=150)
Loss function: Cross-entropy (Further Reading)#
Models that return class probabilities can use cross-entropy loss
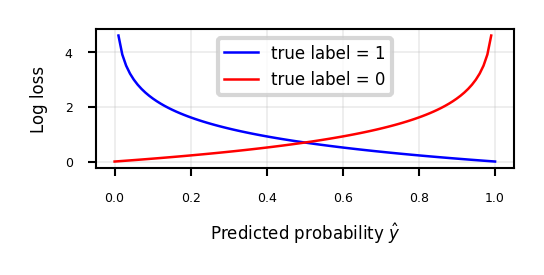
\[\mathcal{L_{log}}(\mathbf{w}) = \sum_{n=1}^{N} H(p_n,q_n) = - \sum_{n=1}^{N} \sum_{c=1}^{C} p_{n,c} log(q_{n,c}) \]Also known as log loss, logistic loss, or maximum likelihood
Based on true probabilities \(p\) (0 or 1) and predicted probabilities \(q\) over \(N\) instances and \(C\) classes
Binary case (C=2): \(\mathcal{L_{log}}(\mathbf{w}) = - \sum_{n=1}^{N} \big[ y_n log(\hat{y}_n) + (1-y_n) log(1-\hat{y}_n) \big]\)
Penalty (or surprise) grows exponentially as difference between \(p\) and \(q\) increases
Often used together with L2 (or L1) loss: \(\mathcal{L_{log}}'(\mathbf{w}) = \mathcal{L_{log}}(\mathbf{w}) + \alpha \sum_{i} w_i^2 \)
We will see this loss function in Deep Learning Course
Show code cell content
def cross_entropy(yHat, y):
if y == 1:
return -np.log(yHat)
else:
return -np.log(1 - yHat)
fig, ax = plt.subplots(figsize=(6*fig_scale,2*fig_scale))
x = np.linspace(0,1,100)
ax.plot(x,cross_entropy(x, 1),lw=2*fig_scale,c='b',label='true label = 1', linestyle='-')
ax.plot(x,cross_entropy(x, 0),lw=2*fig_scale,c='r',label='true label = 0', linestyle='-')
ax.set_xlabel(r"Predicted probability $\hat{y}$")
ax.set_ylabel("Log loss")
plt.grid()
plt.legend();
Optimization methods (solvers) for cross-entropy loss#
Gradient descent (only supports L2 regularization)
Log loss is differentiable, so we can use (stochastic) gradient descent
Variants thereof, e.g. Stochastic Average Gradient (SAG, SAGA)
Coordinate descent (supports both L1 and L2 regularization)
Faster iteration, but may converge more slowly, has issues with saddlepoints
Called
liblinearin sklearn. Can’t run in parallel.
Newton-Rhapson or Newton Conjugate Gradient (only L2):
Uses the Hessian \(H = \big[\frac{\partial^2 \mathcal{L}}{\partial x_i \partial x_j} \big]\): \(\mathbf{w}^{s+1} = \mathbf{w}^s-\eta H^{-1}(\mathbf{w}^s) \nabla \mathcal{L}(\mathbf{w}^s)\)
Slow for large datasets. Works well if solution space is (near) convex
Quasi-Newton methods (only L2)
Approximate, faster to compute
E.g. Limited-memory Broyden–Fletcher–Goldfarb–Shanno (
lbfgs)Default in sklearn for Logistic Regression
For further information about conjugate gradients, see [Nem18]
You will see many of these solvers in Optimization course taught by Dr. Ghanbari.
In practice#
Logistic regression can also be found in
sklearn.linear_model.Chyperparameter is the inverse regularization strength: \(C=\alpha^{-1}\)penalty: type of regularization: L1, L2 (default), Elastic-Net, or Nonesolver: newton-cg, lbfgs (default), liblinear, sag, saga
Increasing C: less regularization, tries to overfit individual points
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(C=1).fit(X_train, y_train)
Show code cell source
from sklearn.linear_model import LogisticRegression
@interact
def plot_lr(C_log=(-3,4,0.1)):
# Still using artificial data
fig, ax = plt.subplots(figsize=(6*fig_scale,3*fig_scale))
mglearn.discrete_scatter(Xf[:, 0], Xf[:, 1], yf, ax=ax, s=10*fig_scale)
lr = LogisticRegression(C=10**C_log).fit(Xf, yf)
w = lr.coef_[0]
xx = np.linspace(7, 13)
yy = (-w[0] * xx - lr.intercept_[0]) / w[1]
ax.plot(xx, yy, c='k')
ax.set_xticks(())
ax.set_yticks(())
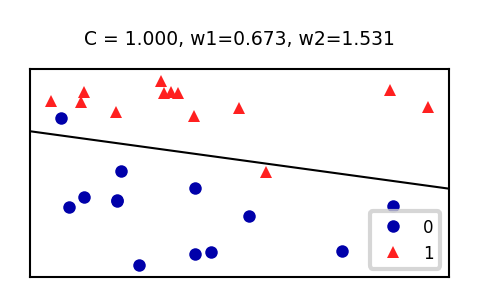
ax.set_title("C = {:.3f}, w1={:.3f}, w2={:.3f}".format(10**C_log,w[0],w[1]))
ax.legend(loc="best");
Show code cell output
Show code cell source
if not interactive:
plot_lr(C_log=(0))
plot_lr(C_log=(4))

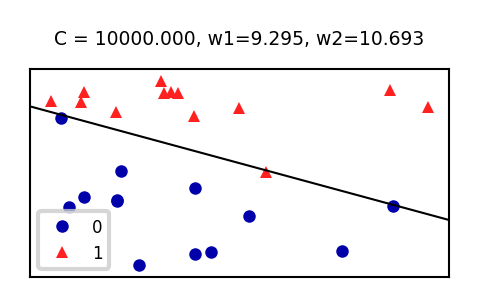
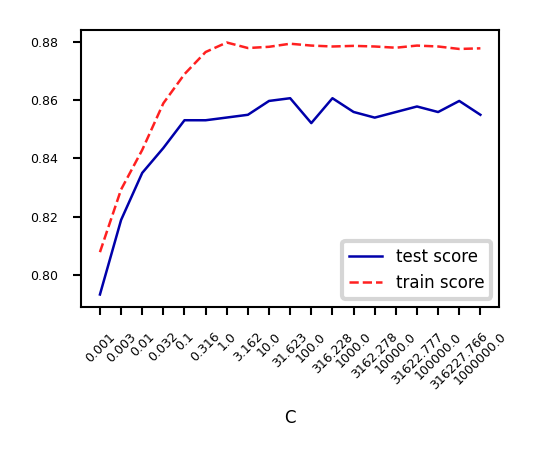
Analyze behavior on the breast cancer dataset
Underfitting if C is too small, some overfitting if C is too large
We use cross-validation because the dataset is small
Show code cell source
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_validate
spam_data = fetch_openml(name="qsar-biodeg", as_frame=True)
X_C, y_C = spam_data.data, spam_data.target
C=np.logspace(-3,6,num=19)
test_score=[]
train_score=[]
for c in C:
lr = LogisticRegression(C=c)
scores = cross_validate(lr,X_C,y_C,cv=10, return_train_score=True)
test_score.append(np.mean(scores['test_score']))
train_score.append(np.mean(scores['train_score']))
fig, ax = plt.subplots(figsize=(6*fig_scale,4*fig_scale))
ax.set_xticks(range(19))
ax.set_xticklabels(np.round(C,3))
ax.set_xlabel('C')
ax.plot(test_score, lw=2*fig_scale, label='test score')
ax.plot(train_score, lw=2*fig_scale, label='train score')
ax.legend()
plt.xticks(rotation=45);
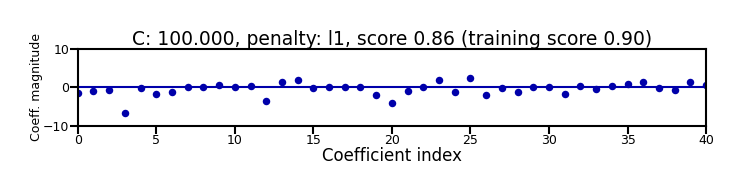
Again, choose between L1 or L2 regularization (or elastic-net)
Small C overfits, L1 leads to sparse models
Show code cell source
X_C_train, X_C_test, y_C_train, y_C_test = train_test_split(X_C, y_C, random_state=0)
@interact
def plot_logreg(C=(0.01,1000.0,0.1), penalty=['l1','l2']):
r = LogisticRegression(C=C, penalty=penalty, solver='liblinear').fit(X_C_train, y_C_train)
fig, ax = plt.subplots(figsize=(8*fig_scale,1.9*fig_scale))
ax.plot(r.coef_.T, 'o', markersize=6*fig_scale)
ax.set_title("C: {:.3f}, penalty: {}, score {:.2f} (training score {:.2f})".format(C, penalty, r.score(X_C_test, y_C_test), r.score(X_C_train, y_C_train)),pad=0)
ax.set_xlabel("Coefficient index", labelpad=0)
ax.set_ylabel("Coeff. magnitude", labelpad=0, fontsize=10*fig_scale)
ax.tick_params(axis='both', pad=0)
ax.hlines(0, 40, len(r.coef_)-1)
ax.set_ylim(-10, 10)
ax.set_xlim(0, 40);
plt.tight_layout();
Show code cell output
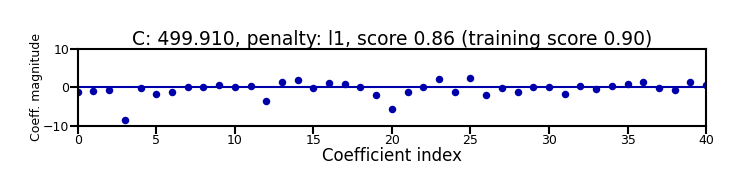
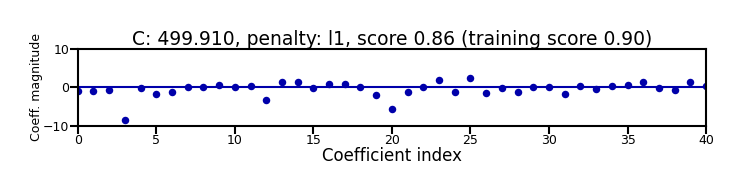
Show code cell source
if not interactive:
plot_logreg(0.001, 'l2')
plot_logreg(100, 'l2')
plot_logreg(100, 'l1')
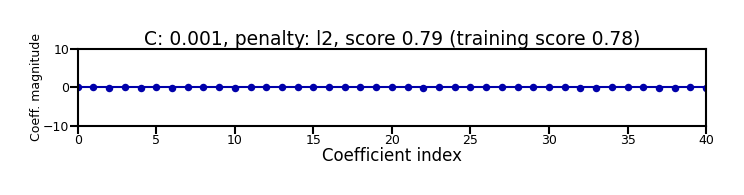
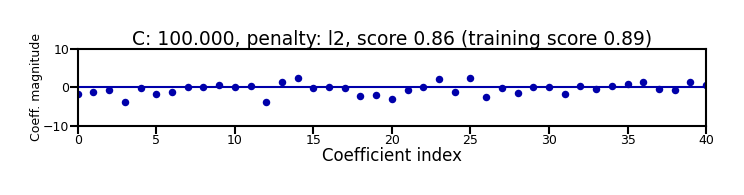
Note: Data scaling helps convergence, minimizes differences between solvers
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_classification
# Generate data with unscaled features
X, y = make_classification(n_features=2, n_redundant=0, random_state=42)
X[:, 1] *= 1000 # Artificially scale one feature
# Solvers to compare
solvers = ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga']
# Without scaling
for solver in solvers:
model = LogisticRegression(solver=solver, max_iter=1000)
model.fit(X, y)
print(f"{solver:10} → Iterations: {model.n_iter_[0]} (unscaled)")
# With scaling
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
for solver in solvers:
model = LogisticRegression(solver=solver, max_iter=1000)
model.fit(X_scaled, y)
print(f"{solver:10} → Iterations: {model.n_iter_[0]} (scaled)")
newton-cg → Iterations: 19 (unscaled)
lbfgs → Iterations: 43 (unscaled)
liblinear → Iterations: 14 (unscaled)
sag → Iterations: 1000 (unscaled)
saga → Iterations: 1000 (unscaled)
newton-cg → Iterations: 5 (scaled)
lbfgs → Iterations: 7 (scaled)
liblinear → Iterations: 5 (scaled)
sag → Iterations: 21 (scaled)
saga → Iterations: 12 (scaled)
Ridge Classification#
Instead of log loss, we can also use ridge loss:
\[\mathcal{L}_{Ridge} = \sum_{n=1}^{N} (y_n-(\mathbf{w}\mathbf{x_n} + w_0))^2 + \alpha \sum_{i=1}^{p} w_i^2\]In this case, target values {negative, positive} are converted to {-1,1}
Can be solved similarly to Ridge regression:
Closed form solution (a.k.a. Cholesky)
Gradient descent and variants
E.g. Conjugate Gradient (CG) or Stochastic Average Gradient (SAG,SAGA)
Use Cholesky for smaller datasets, Gradient descent for larger ones
Linear Models for multiclass classification#
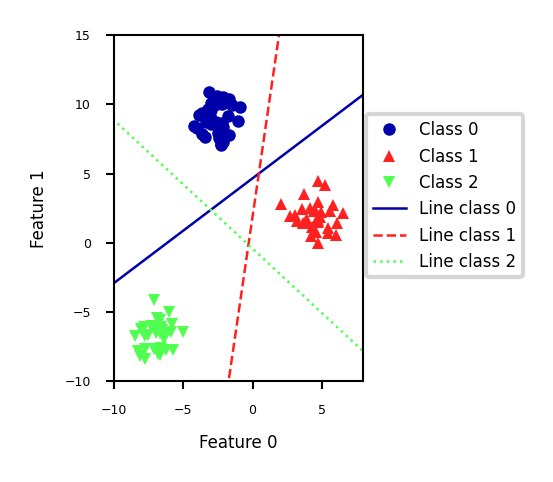
one-vs-rest (aka one-vs-all)#
Learn a binary model for each class vs. all other classes
Create as many binary models as there are classes
Show code cell source
from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
linear_svm = LinearSVC().fit(X, y)
plt.rcParams["figure.figsize"] = (7*fig_scale,5*fig_scale)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, s=10*fig_scale)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color, lw=2*fig_scale)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.gca().set_aspect('equal')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
'Line class 2'], loc=(1.01, 0.3))
<matplotlib.legend.Legend at 0x226687e4970>
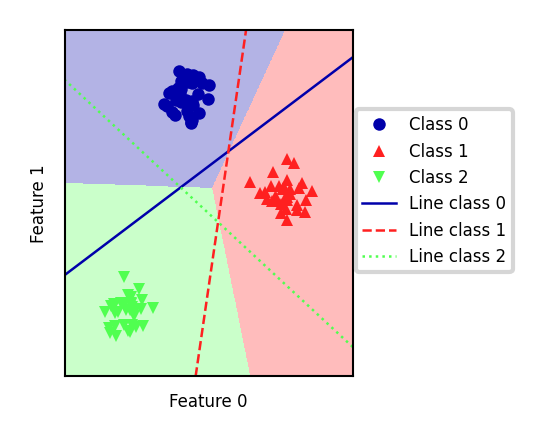
Every binary classifiers makes a prediction, the one with the highest score (>0) wins
Show code cell source
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=0.3)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, s=10*fig_scale)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color, lw=2*fig_scale)
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Line class 0', 'Line class 1',
'Line class 2'], loc=(1.01, 0.3))
plt.gca().set_aspect('equal')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
Text(0, 0.5, 'Feature 1')
one-vs-one#
An alternative is to learn a binary model for every combination of two classes
For \(C\) classes, this results in \(\frac{C(C-1)}{2}\) binary models
Each point is classified according to a majority vote amongst all models
Can also be a ‘soft vote’: sum up the probabilities (or decision values) for all models. The class with the highest sum wins.
Requires more models than one-vs-rest, but training each one is faster
Only the examples of 2 classes are included in the training data
Recommended for algorithms than learn well on small datasets
Especially SVMs and Gaussian Processes
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.multiclass import OneVsOneClassifier
import mglearn
# Generate synthetic dataset
X, y = make_blobs(random_state=42)
# Apply One-vs-One classification using SVM
ovo_svm = OneVsOneClassifier(SVC(kernel="linear")).fit(X, y)
# Plot decision boundaries with one-vs-one classifier
mglearn.plots.plot_2d_classification(ovo_svm, X, fill=True, alpha=0.3)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, s=10*fig_scale)
# Generate decision boundaries for each binary classifier
line = np.linspace(-15, 15)
for estimator, color in zip(ovo_svm.estimators_, mglearn.cm3.colors):
coef = estimator.coef_[0]
intercept = estimator.intercept_[0]
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color, lw=2*fig_scale)
# Set aspect ratio to ensure unit distances appear equal
plt.gca().set_aspect('equal')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.legend(['Class 0', 'Class 1', 'Class 2', 'Binary decision boundaries'], loc=(1.01, 0.3))
plt.show()
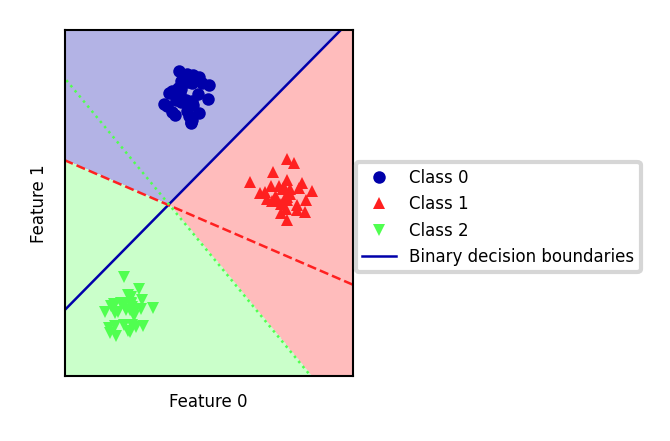
Show code cell source
%%HTML
<style>
td {font-size: 16px}
th {font-size: 16px}
.rendered_html table, .rendered_html td, .rendered_html th {
font-size: 16px;
}
</style>
Linear models overview#
Name |
Representation |
Loss function |
Optimization |
Regularization |
|---|---|---|---|---|
Least squares |
Linear function (R) |
SSE |
CFS or SGD |
None |
Ridge |
Linear function (R) |
SSE + L2 |
CFS or SGD |
L2 strength (\(\alpha\)) |
Lasso |
Linear function (R) |
SSE + L1 |
Coordinate descent |
L1 strength (\(\alpha\)) |
Elastic-Net |
Linear function (R) |
SSE + L1 + L2 |
Coordinate descent |
\(\alpha\), L1 ratio (\(\rho\)) |
SGDRegressor |
Linear function (R) |
SSE, Huber, \(\epsilon\)-ins,… + L1/L2 |
SGD |
L1/L2, \(\alpha\) |
Logistic regression |
Linear function (C) |
Log + L1/L2 |
SGD, coordinate descent,… |
L1/L2, \(\alpha\) |
Ridge classification |
Linear function (C) |
SSE + L2 |
CFS or SGD |
L2 strength (\(\alpha\)) |
Linear SVM |
Support Vectors |
Hinge(1) |
Quadratic programming or SGD |
Cost (C) |
Least Squares SVM |
Support Vectors |
Squared Hinge |
Linear equations or SGD |
Cost (C) |
Perceptron |
Linear function (C) |
Hinge(0) |
SGD |
None |
SGDClassifier |
Linear function (C) |
Log, (Sq.) Hinge, Mod. Huber,… |
SGD |
L1/L2, \(\alpha\) |
SSE: Sum of Squared Errors
CFS: Closed-form solution
SGD: (Stochastic) Gradient Descent and variants
(R)egression, (C)lassification
Summary#
Linear models
Good for very large datasets (scalable)
Good for very high-dimensional data (not for low-dimensional data)
Can be used to fit non-linear or low-dim patterns as well (see later)
Preprocessing: e.g. Polynomial or Poisson transformations
Generalized linear models (kernel trick)
Regularization is important. Tune the regularization strength (\(\alpha\))
Ridge (L2): Good fit, sometimes sensitive to outliers
Lasso (L1): Sparse models: fewer features, more interpretable, faster
Elastic-Net: Trade-off between both, e.g. for correlated features
Most can be solved by different optimizers (solvers)
Closed form solutions or quadratic/linear solvers for smaller datasets
Gradient descent variants (SGD,CD,SAG,CG,…) for larger ones
Multi-class classification can be done using a one-vs-all approach
Please refer to Appendix for further information about SVM.

