Lecture 1: Introduction

Lecture 1: Introduction#

A few useful things to know about machine learning

Mahmood Amintoosi, Spring 2024

Computer Science Dept, Ferdowsi University of Mashhad

I should mention that the original material of this course was from Open Machine Learning Course, by Joaquin Vanschoren and others.

Why Machine Learning?#

Search engines (e.g. Google)
Recommender systems (e.g. Netflix)
Automatic translation (e.g. Google Translate)
Speech understanding (e.g. Siri, Alexa)
Game playing (e.g. AlphaGo)
Self-driving cars
Personalized medicine
Progress in all sciences: Genetics, astronomy, chemistry, neurology, physics,…

What is Machine Learning?#

Learn to perform a task, based on experience (examples) \(X\), minimizing error \(\mathcal{E}\)
- E.g. recognizing a person in an image as accurately as possible
Often, we want to learn a function (model) \(f\) with some model parameters \(\theta\) that produces the right output \(y\)

\[f_{\theta}(X) = y\]

\[\underset{\theta}{\operatorname{argmin}} \mathcal{E}(f_{\theta}(X))\]

Usually part of a much larger system that provides the data \(X\) in the right form
- Data needs to be collected, cleaned, normalized, checked for data biases,…

Inductive bias#

In practice, we have to put assumptions into the model: inductive bias \(b\)
- What should the model look like?
  - Mimick human brain: Neural Networks
  - Logical combination of inputs: Decision trees, Linear models
  - Remember similar examples: Nearest Neighbors, SVMs
  - Probability distribution: Bayesian models
- User-defined settings (hyperparameters)
  - E.g. depth of tree, network architecture
- Assuptions about the data distribution, e.g. \(X \sim N(\mu,\sigma)\)
We can transfer knowledge from previous tasks: \(f_1, f_2, f_3, ... \Longrightarrow f_{new}\)
- Choose the right model, hyperparameters
- Reuse previously learned values for model parameters \(\theta\)
In short:

\[\underset{\theta,b}{\operatorname{argmin}} \mathcal{E}(f_{\theta, b}(X))\]

Machine learning vs Statistics#

See Breiman (2001): Statistical modelling: The two cultures
Both aim to make predictions of natural phenomena:
Statistics:
- Help humans understand the world
- Assume data is generated according to an understandable model
Machine learning:
- Automate a task entirely (partially replace the human)
- Assume that the data generation process is unknown
- Engineering-oriented, less (too little?) mathematical theory

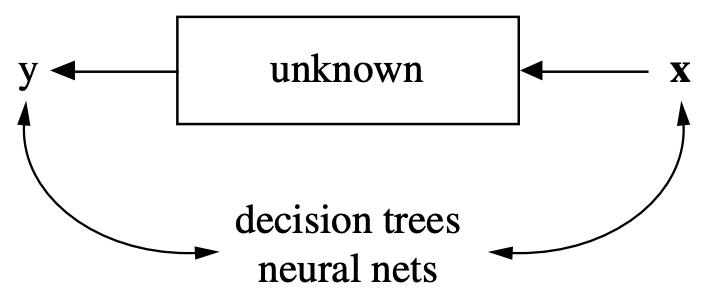
Types of machine learning#

Supervised Learning: learn a model \(f\) from labeled data \((X,y)\) (ground truth)
- Given a new input X, predict the right output y
- Given examples of stars and galaxies, identify new objects in the sky
Unsupervised Learning: explore the structure of the data (X) to extract meaningful information
- Given inputs X, find which ones are special, similar, anomalous, …
Semi-Supervised Learning: learn a model from (few) labeled and (many) unlabeled examples
- Unlabeled examples add information about which new examples are likely to occur
Reinforcement Learning: develop an agent that improves its performance based on interactions with the environment

Note: Practical ML systems can combine many types in one system.

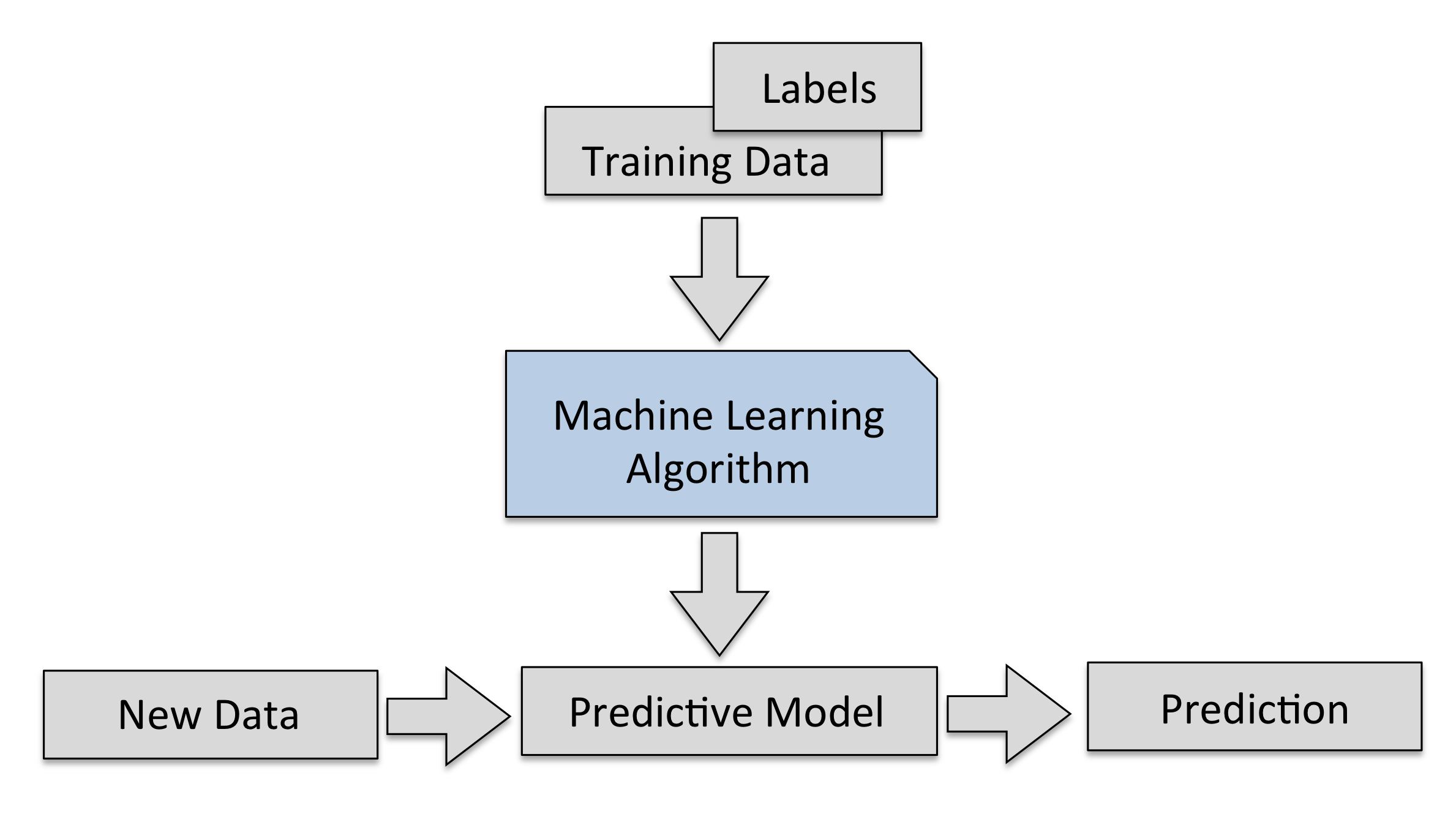
Supervised Machine Learning#

Learn a model from labeled training data, then make predictions
Supervised: we know the correct/desired outcome (label)
Subtypes: classification (predict a class) and regression (predict a numeric value)
Most supervised algorithms that we will see can do both

Classification#

Predict a class label (category), discrete and unordered
- Can be binary (e.g. spam/not spam) or multi-class (e.g. letter recognition)
- Many classifiers can return a confidence per class
The predictions of the model yield a decision boundary separating the classes

_images/3e4bb1a4e9adab97d6b437af7df0b1e582038033d6420024431c0bc5361c3345.png

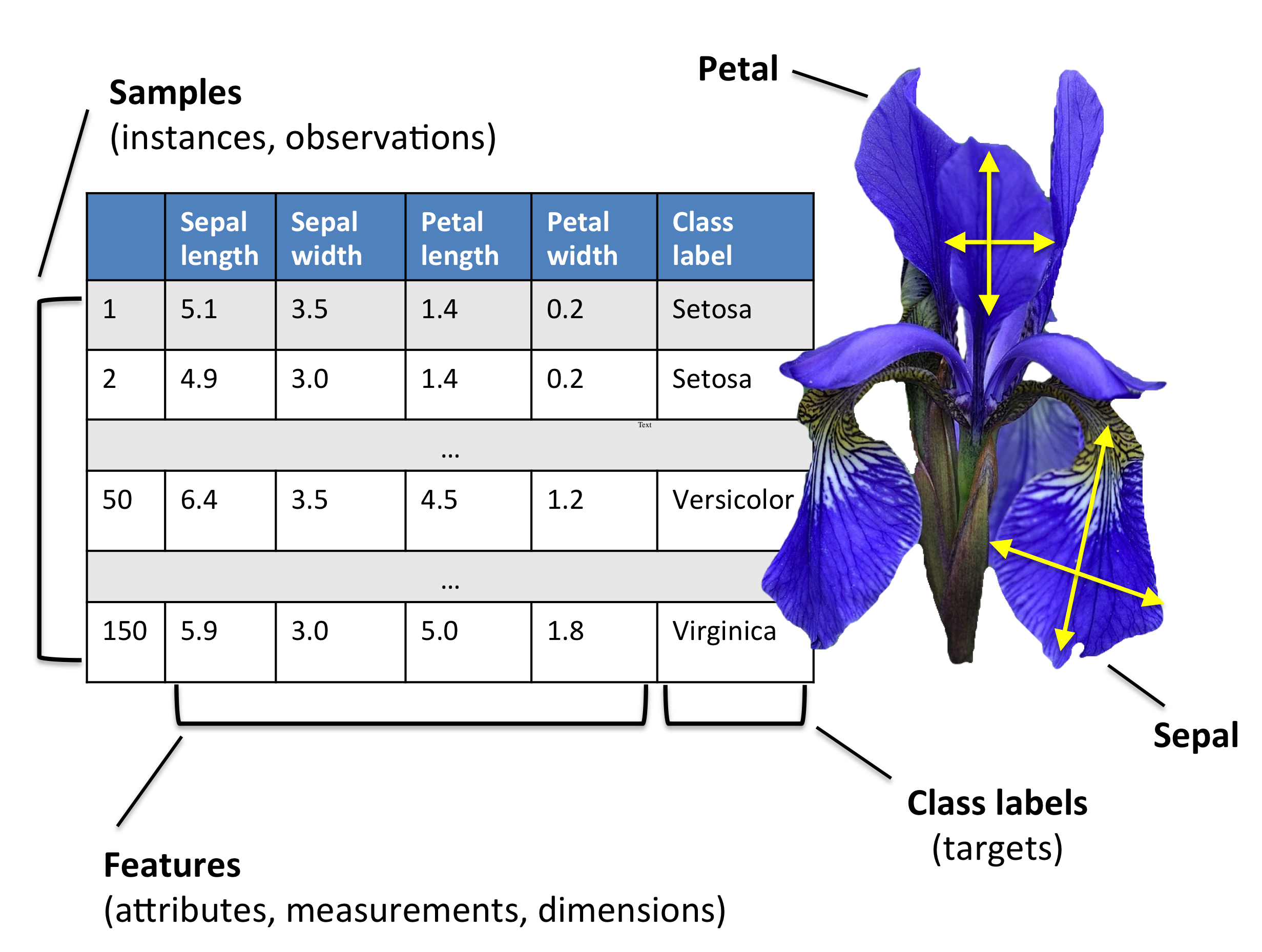
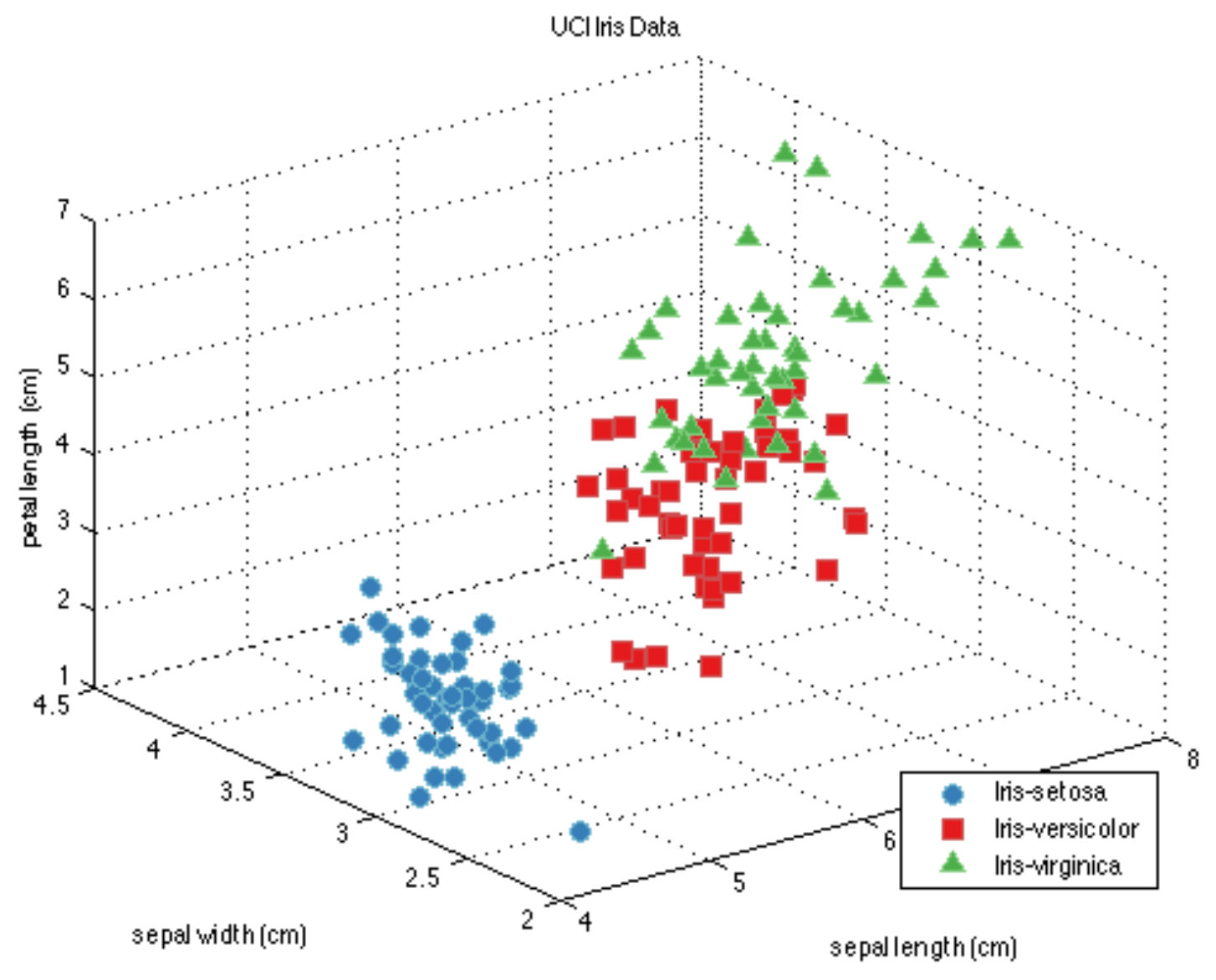
Example: Flower classification#

Classify types of Iris flowers (setosa, versicolor, or virginica). How would you do it?

Representation: input features and labels#

We could take pictures and use them (pixel values) as inputs (-> Deep Learning)
We can manually define a number of input features (variables), e.g. length and width of leaves
Every `example’ is a point in a (possibly high-dimensional) space

Regression#

Predict a continuous value, e.g. temperature
- Target variable is numeric
- Some algorithms can return a confidence interval
Find the relationship between predictors and the target.

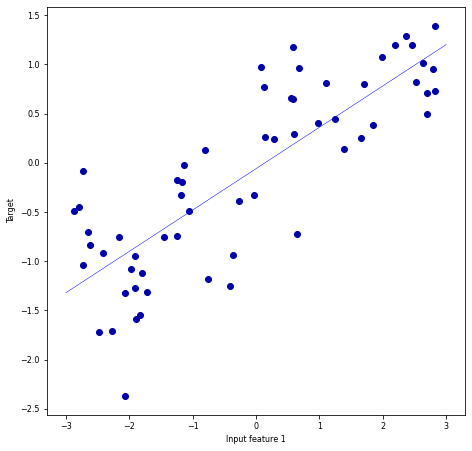
_images/c12e22fa7f6823269bab55b1ea070b896860cfa3c34c235e1776a294acb5d5f1.png

Unsupervised Machine Learning#

Unlabeled data, or data with unknown structure
Explore the structure of the data to extract information
Many types, we’ll just discuss two.

Clustering#

Organize information into meaningful subgroups (clusters)
Objects in cluster share certain degree of similarity (and dissimilarity to other clusters)
Example: distinguish different types of customers

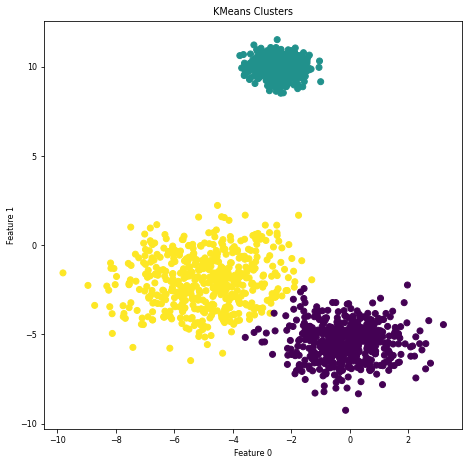
_images/da8b156a137054a2de00958c84e3ea4e45f2c02bdbce2bd28cb42c2344f697ed.png

Dimensionality reduction#

Data can be very high-dimensional and difficult to understand, learn from, store,…
Dimensionality reduction can compress the data into fewer dimensions, while retaining most of the information
Contrary to feature selection, the new features lose their (original) meaning
The new representation can be a lot easier to model (and visualize)

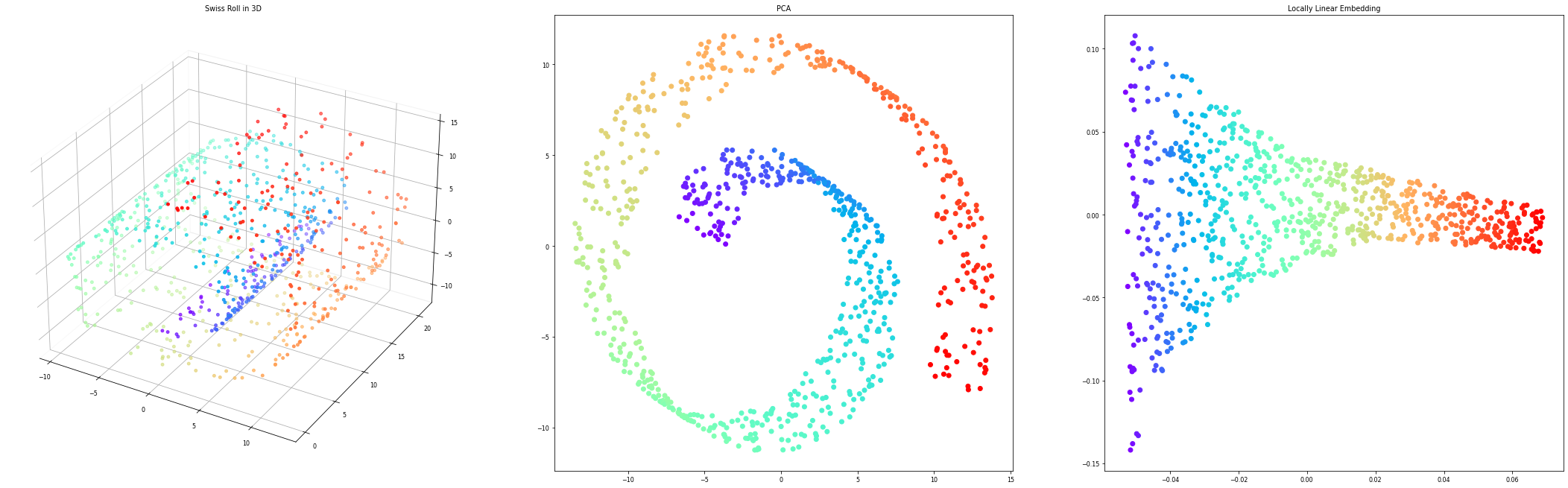
_images/5eeb6c9affdf1d77d98f9e3d63975e0068444441b7516b878ba776471068fb88.png

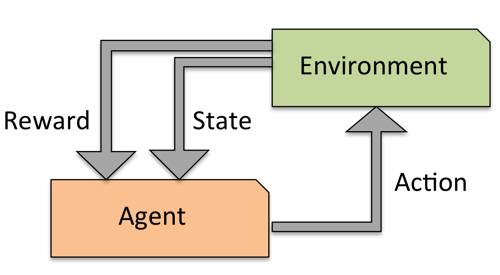
Reinforcement learning#

Develop an agent that improves its performance based on interactions with the environment
- Example: games like Chess, Go,…
Search a (large) space of actions and states
Reward function defines how well a (series of) actions works
Learn a series of actions (policy) that maximizes reward through exploration

Learning = Representation + evaluation + optimization#

All machine learning algorithms consist of 3 components:

Representation: A model \(f_{\theta}\) must be represented in a formal language that the computer can handle
- Defines the ‘concepts’ it can learn, the hypothesis space
- E.g. a decision tree, neural network, set of annotated data points
Evaluation: An internal way to choose one hypothesis over the other
- Objective function, scoring function, loss function \(\mathcal{L}(f_{\theta})\)
- E.g. Difference between correct output and predictions
Optimization: An efficient way to search the hypothesis space
- Start from simple hypothesis, extend (relax) if it doesn’t fit the data
- Start with initial set of model parameters, gradually refine them
- Many methods, differing in speed of learning, number of optima,…

A powerful/flexible model is only useful if it can also be optimized efficiently

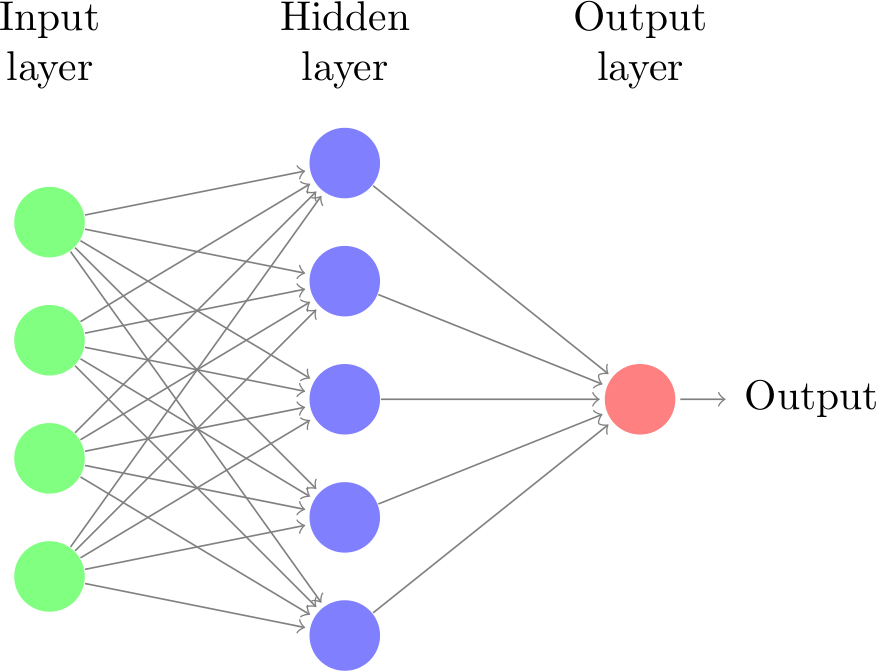
Neural networks: representation#

Let’s take neural networks as an example

Representation: (layered) neural network
- Each connection has a weight \(\theta_i\) (a.k.a. model parameters)
- Each node receives weighted inputs, emits new value
- Model \(f\) returns the output of the last layer
The architecture, number/type of neurons, etc. are fixed
- We call these hyperparameters (set by user, fixed during training)

Neural networks: evaluation and optimization#

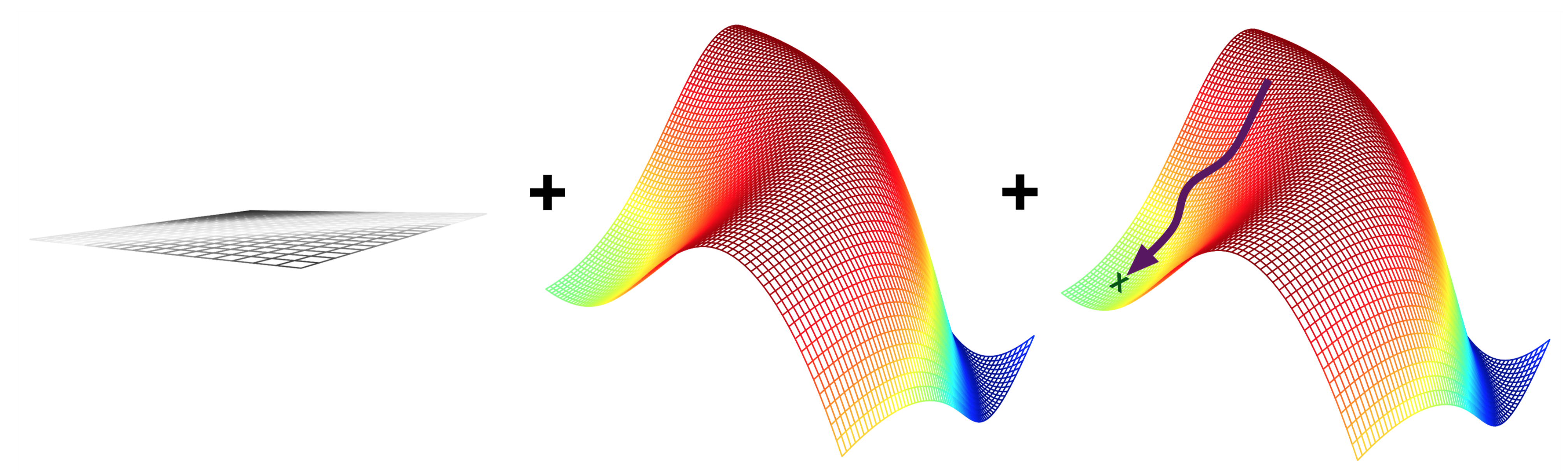
Representation: Given the structure, the model is represented by its parameters
- Imagine a mini-net with two weights (\(\theta_0,\theta_1\)): a 2-dimensional search space
Evaluation: A loss function \(\mathcal{L}(\theta)\) computes how good the predictions are
- Estimated on a set of training data with the ‘correct’ predictions
- We can’t see the full surface, only evaluate specific sets of parameters
Optimization: Find the optimal set of parameters
- Usually a type of search in the hypothesis space
- E.g. Gradient descent: \(\theta_i^{new} = \theta_i - \frac{\partial \mathcal{L}(\theta)}{\partial \theta_i} \)

Overfitting and Underfitting#

It’s easy to build a complex model that is 100% accurate on the training data, but very bad on new data
Overfitting: building a model that is too complex for the amount of data you have
- You model peculiarities in your training data (noise, biases,…)
- Solve by making model simpler (regularization), or getting more data
- Most algorithms have hyperparameters that allow regularization
Underfitting: building a model that is too simple given the complexity of the data
- Use a more complex model
There are techniques for detecting overfitting (e.g. bias-variance analysis). More about that later
You can build ensembles of many models to overcome both underfitting and overfitting

There is often a sweet spot that you need to find by optimizing the choice of algorithms and hyperparameters, or using more data.
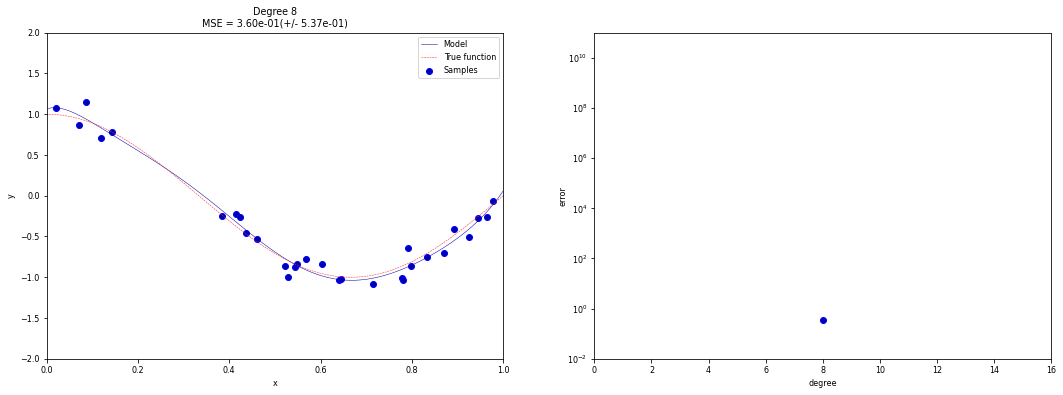
Example: regression using polynomial functions

Show code cell source Hide code cell source

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score

def true_fun(X):
    return np.cos(1.5 * np.pi * X)

np.random.seed(0)
n_samples = 30
X3 = np.sort(np.random.rand(n_samples))
y3 = true_fun(X3) + np.random.randn(n_samples) * 0.1
X3_test = np.linspace(0, 1, 100)
scores_x, scores_y = [], []

show_output = True

@interact
def plot_poly(degrees = (1, 16, 1)):
    polynomial_features = PolynomialFeatures(degree=degrees,
                                             include_bias=False)
    linear_regression = LinearRegression()
    pipeline = Pipeline([("polynomial_features", polynomial_features),
                         ("linear_regression", linear_regression)])
    pipeline.fit(X3[:, np.newaxis], y3)

    # Evaluate the models using crossvalidation
    scores = cross_val_score(pipeline, X3[:, np.newaxis], y3,
                             scoring="neg_mean_squared_error", cv=10)   
    scores_x.append(degrees)
    scores_y.append(-scores.mean())

    if show_output:
        fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12*fig_scale, 4*fig_scale))    
        ax1.plot(X3_test, pipeline.predict(X3_test[:, np.newaxis]), label="Model")
        ax1.plot(X3_test, true_fun(X3_test), label="True function")
        ax1.scatter(X3, y3, edgecolor='b', label="Samples")
        ax1.set_xlabel("x")
        ax1.set_ylabel("y")
        ax1.set_xlim((0, 1))
        ax1.set_ylim((-2, 2))
        ax1.legend(loc="best")
        ax1.set_title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(
            degrees, -scores.mean(), scores.std()))

        # Plot scores
        ax2.scatter(scores_x, scores_y, edgecolor='b')
        order = np.argsort(scores_x)
        ax2.plot(np.array(scores_x)[order], np.array(scores_y)[order])
        ax2.set_xlim((0, 16))
        ax2.set_ylim((10**-2, 10**11))
        ax2.set_xlabel("degree")
        ax2.set_ylabel("error", labelpad=0)
        ax2.set_yscale("log")

        fig.show()

_images/a3de474646bca7a07b8f525f01b34fc853f99fcb4b0fb749203d78712ed54eb1.png

Model selection#

Next to the (internal) loss function, we need an (external) evaluation function
- Feedback signal: are we actually learning the right thing?
  - Are we under/overfitting?
- Carefully choose to fit the application.
- Needed to select between models (and hyperparameter settings)

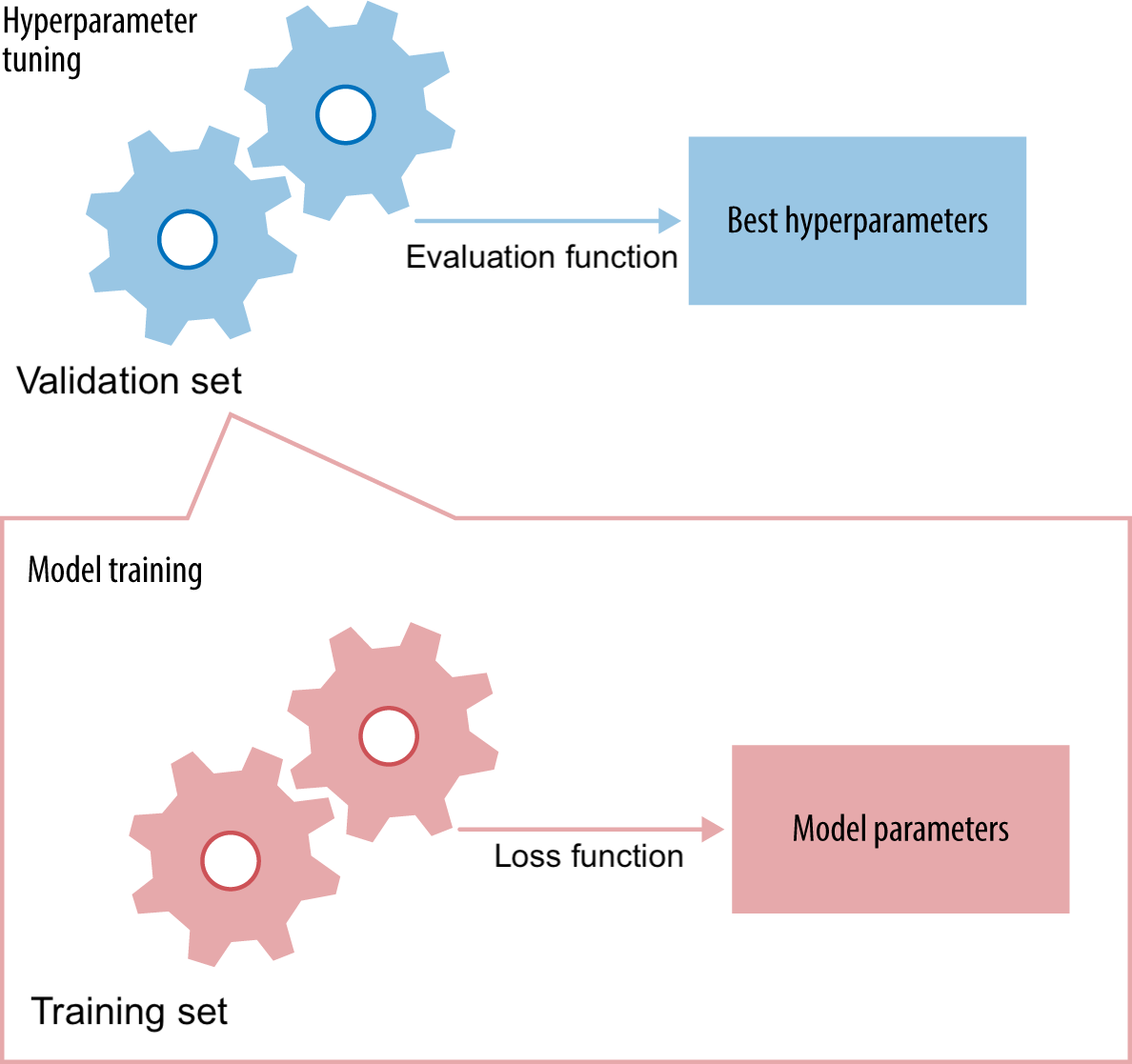
Data needs to be split into training and test sets
- Optimize model parameters on the training set, evaluate on independent test set
Avoid data leakage:
- Never optimize hyperparameter settings on the test data
- Never choose preprocessing techniques based on the test data
To optimize hyperparameters and preprocessing as well, set aside part of training set as a validation set
- Keep test set hidden during all training

_images/4ba5ffaf344e92feadb5192c0ea68719725994ebfc3a51c6537595969510615d.png

For a given hyperparameter setting, learn the model parameters on training set
- Minize the loss
Evaluate the trained model on the validation set
- Tune the hyperparameters to maximize a certain metric (e.g. accuracy)

Only generalization counts!#

Never evaluate your final models on the training data, except for:
- Tracking whether the optimizer converges (learning curves)
- Diagnosing under/overfitting:
  - Low training and test score: underfitting
  - High training score, low test score: overfitting
Always keep a completely independent test set
On small datasets, use multiple train-test splits to avoid sampling bias
- You could sample an ‘easy’ test set by accident
- E.g. Use cross-validation (see later)

Better data representations, better models#

Algorithm needs to correctly transform the inputs to the right outputs
A lot depends on how we present the data to the algorithm
- Transform data to better representation (a.k.a. encoding or embedding)
- Can be done end-to-end (e.g. deep learning) or by first ‘preprocessing’ the data (e.g. feature selection/generation)

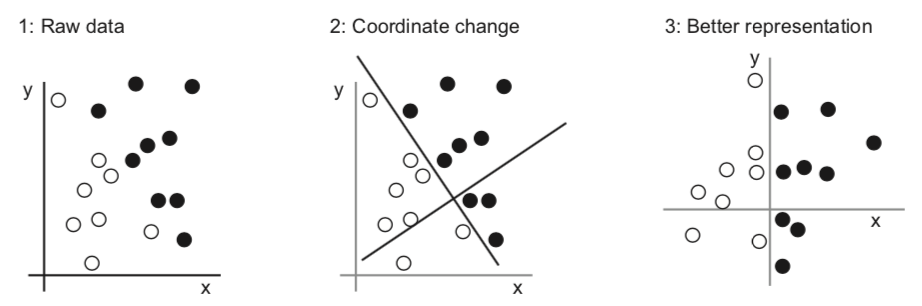
Feature engineering#

Most machine learning techniques require humans to build a good representation of the data
Especially when data is naturally structured (e.g. table with meaningful columns)
Feature engineering is often still necessary to get the best results
- Feature selection, dimensionality reduction, scaling, …
- Applied machine learning is basically feature engineering (Andrew Ng)
Nothing beats domain knowledge (when available) to get a good representation
- E.g. Iris data: leaf length/width separate the classes well

Build prototypes early-on

Learning data transformations end-to-end#

For unstructured data (e.g. images, text), it’s hard to extract good features
Deep learning: learn your own representation (embedding) of the data
- Through multiple layers of representation (e.g. layers of neurons)
- Each layer transforms the data a bit, based on what reduces the error

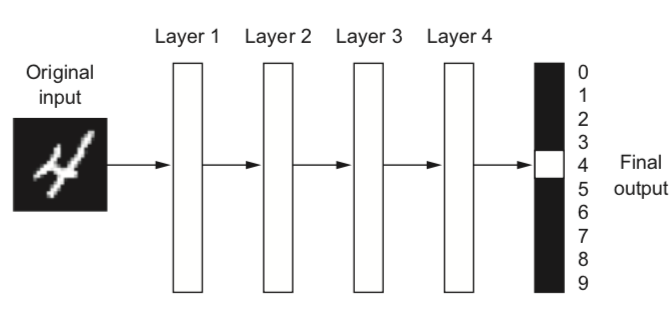
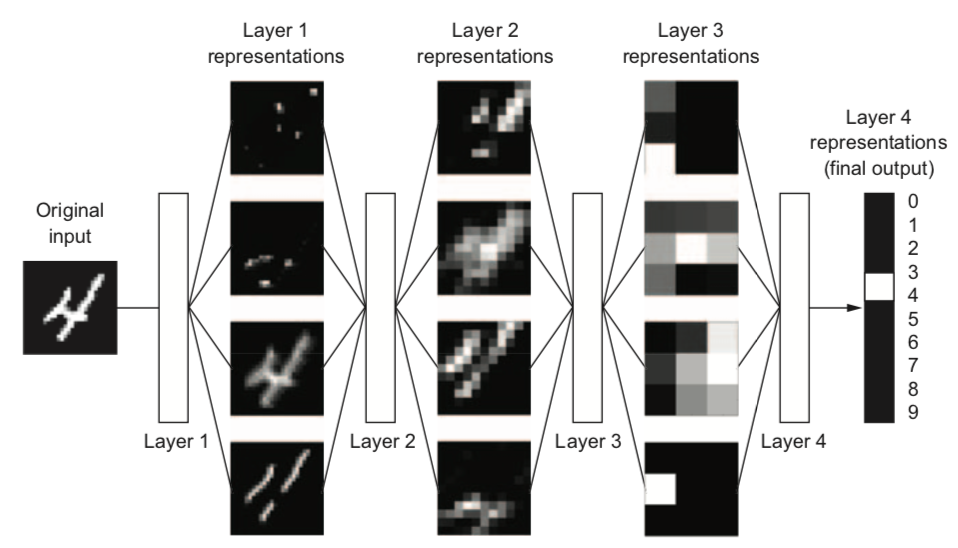
Example: digit classification#

Input pixels go in, each layer transforms them to an increasingly informative representation for the given task
Often less intuitive for humans

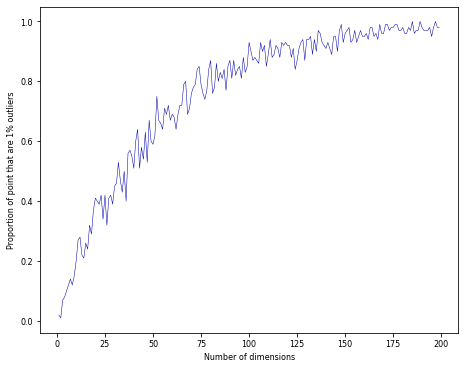
Curse of dimensionality#

Just adding lots of features and letting the model figure it out doesn’t work
Our assumptions (inductive biases) often fail in high dimensions:
- Randomly sample points in an n-dimensional space (e.g. a unit hypercube)
- Almost all points become outliers at the edge of the space
- Distances between any two points will become almost identical

_images/a9475958cc1415145d01fb343846809a33edfc7e8bdc5af5645a46af916fe88c.png

Practical consequences#

For every dimension (feature) you add, you need exponentially more data to avoid sparseness
Affects any algorithm that is based on distances (e.g. kNN, SVM, kernel-based methods, tree-based methods,…)
Blessing of non-uniformity: on many applications, the data lives in a very small subspace
- You can drastically improve performance by selecting features or using lower-dimensional data representations

“More data can beat a cleverer algorithm”#

(but you need both)

More data reduces the chance of overfitting
Less sparse data reduces the curse of dimensionality
Non-parametric models: number of model parameters grows with amount of data
- Tree-based techniques, k-Nearest neighbors, SVM,…
- They can learn any model given sufficient data (but can get stuck in local minima)
Parametric (fixed size) models: fixed number of model parameters
- Linear models, Neural networks,…
- Can be given a huge number of parameters to benefit from more data
- Deep learning models can have millions of weights, learn almost any function.
The bottleneck is moving from data to compute/scalability

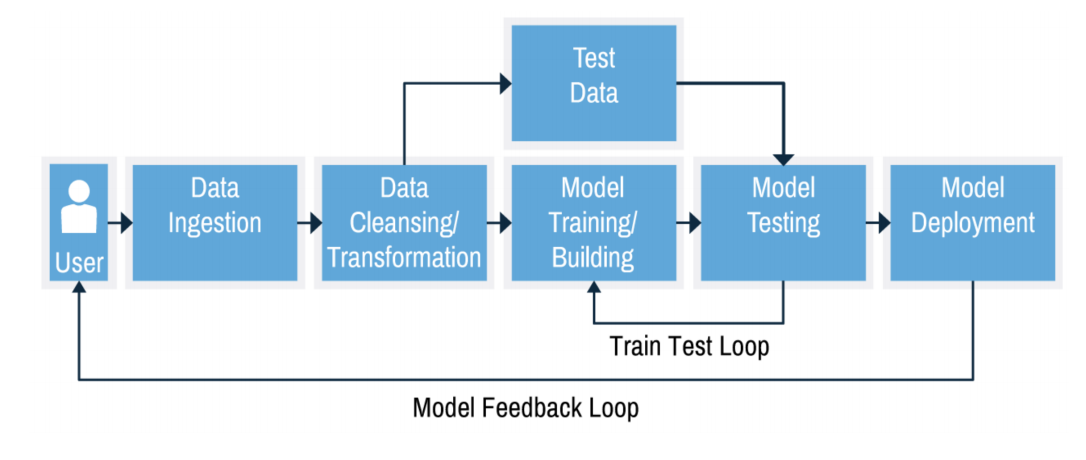
Building machine learning systems#

A typical machine learning system has multiple components, which we will cover in upcoming lectures:

Preprocessing: Raw data is rarely ideal for learning
- Feature scaling: bring values in same range
- Encoding: make categorical features numeric
- Discretization: make numeric features categorical
- Label imbalance correction (e.g. downsampling)
- Feature selection: remove uninteresting/correlated features
- Dimensionality reduction can also make data easier to learn
- Using pre-learned embeddings (e.g. word-to-vector, image-to-vector)

Learning and evaluation
- Every algorithm has its own biases
- No single algorithm is always best
- Model selection compares and selects the best models
  - Different algorithms, different hyperparameter settings
- Split data in training, validation, and test sets
Prediction
- Final optimized model can be used for prediction
- Expected performance is performance measured on independent test set

Together they form a workflow of pipeline
There exist machine learning methods to automatically build and tune these pipelines
You need to optimize pipelines continuously
- Concept drift: the phenomenon you are modelling can change over time
- Feedback: your model’s predictions may change future data

Summary#

Learning algorithms contain 3 components:
- Representation: a model \(f\) that maps input data \(X\) to desired output \(y\)
  - Contains model parameters \(\theta\) that can be made to fit the data \(X\)
- Loss function \(\mathcal{L}(f_{\theta}(X))\): measures how well the model fits the data
- Optimization technique to find the optimal \(\theta\): \(\underset{\theta}{\operatorname{argmin}} \mathcal{L}(f_{\theta}(X))\)
Select the right model, then fit it to the data to minimize a task-specific error \(\mathcal{E}\)
- Inductive bias \(b\): assumptions about model and hyperparameters
  \(\underset{\theta,b}{\operatorname{argmin}} \mathcal{E}(f_{\theta, b}(X))\)
Overfitting: model fits the training data well but not new (test) data
- Split the data into (multiple) train-validation-test splits
- Regularization: tune hyperparameters (on validation set) to simplify model
- Gather more data, or build ensembles of models
Machine learning pipelines: preprocessing + learning + deployment