Appendix A: Kernel SVM and Kernel Regression

Appendix A: Kernel SVM and Kernel Regression#

Computer Science Dept, Ferdowsi University of Mashhad

I should mention that the original material of this course was from Open Machine Learning Course, by Joaquin Vanschoren and others.

Example: SVMs#

Linear SVMs (dual form, for $l$ support vectors with dual coefficients $a_i$ and classes $y_i$):

\[\mathcal{L}_{Dual} (a_i) = \sum_{i=1}^{l} a_i - \frac{1}{2} \sum_{i,j=1}^{l} a_i a_j y_i y_j (\mathbf{x_i} . \mathbf{x_j}) \]

Kernelized SVM, using any existing kernel $k$ we want:

\[\mathcal{L}_{Dual} (a_i, k) = \sum_{i=1}^{l} a_i - \frac{1}{2} \sum_{i,j=1}^{l} a_i a_j y_i y_j k(\mathbf{x_i},\mathbf{x_j}) \]

Show code cell source Hide code cell source

from sklearn import svm

def plot_svm_kernels(kernels, poly_degree=3, gamma=2, C=1, size=4):
    # Our dataset and targets
    X = np.c_[(.4, -.7),
              (-1.5, -1),
              (-1.4, -.9),
              (-1.3, -1.2),
              (-1.1, -.2),
              (-1.2, -.4),
              (-.5, 1.2),
              (-1.5, 2.1),
              (1, 1),
              # --
              (1.3, .8),
              (1.2, .5),
              (.2, -2),
              (.5, -2.4),
              (.2, -2.3),
              (0, -2.7),
              (1.3, 2.1)].T
    Y = [0] * 8 + [1] * 8

    # figure number
    fig, axes = plt.subplots(-(-len(kernels)//3), min(len(kernels),3), figsize=(min(len(kernels),3)*size*1.2*fig_scale, -(-len(kernels)//3)*size*fig_scale), tight_layout=True)
    if len(kernels) == 1:
        axes = np.array([axes])
    if not isinstance(gamma,list):
        gamma = [gamma]*len(kernels)
    if not isinstance(C,list):
        C = [C]*len(kernels)
    # fit the model
    for kernel, ax, g, c in zip(kernels,axes.reshape(-1),gamma,C):
        clf = svm.SVC(kernel=kernel, gamma=g, C=c, degree=poly_degree)
        clf.fit(X, Y)

        # plot the line, the points, and the nearest vectors to the plane
        if kernel == 'rbf':
            ax.set_title(r"kernel = {}, $\gamma$={}, C={}".format(kernel, g, c), pad=0.1)
        else:
            ax.set_title('kernel = %s' % kernel,pad=0.1)

        ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
                    s=25, edgecolors='grey', c='w', zorder=10, linewidths=0.5)
        ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.bwr, s=10*fig_scale)

        for i, coef in enumerate(clf.dual_coef_[0]):
            ax.annotate("%0.2f" % (coef), (clf.support_vectors_[i, 0]+0.1,clf.support_vectors_[i, 1]+0.25), zorder=11, fontsize=3)

        ax.axis('tight')
        x_min = -3
        x_max = 3
        y_min = -3
        y_max = 3

        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
        Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()])

        # Put the result into a color plot
        Z = Z.reshape(XX.shape)
        #plt.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.bwr, alpha=0.1)
        ax.contour(XX, YY, Z, colors=['k', 'k', 'k', 'k', 'k'], linestyles=['--', ':', '-', ':', '--'],
                    levels=[-1, -0.5, 0, 0.5, 1])

        ax.set_xlim(x_min, x_max)
        ax.set_ylim(y_min, y_max)

        ax.set_xticks([])
        ax.set_yticks([])

    plt.tight_layout()
    plt.show()
plot_svm_kernels(['linear', 'poly'],poly_degree=3,size=3.5)

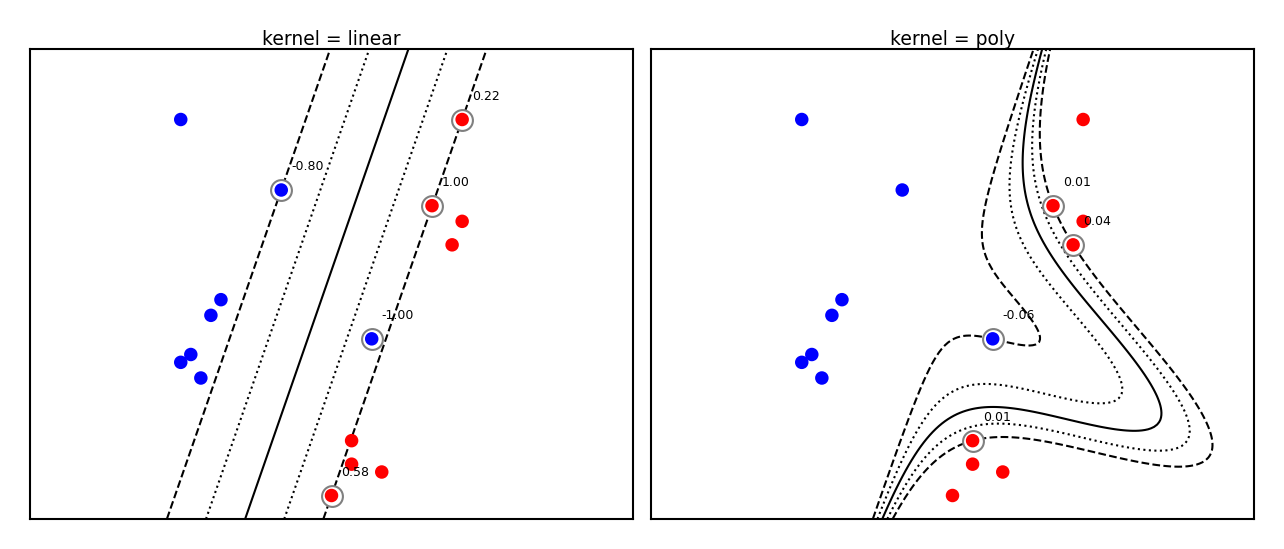
_images/c46af82280cf6dcae058e5b37168f0768b4d4b1c958c8e89cc7888b2a5dea03f.png

Which kernels exist?#

A (Mercer) kernel is any function $k: X \times X \rightarrow \mathbb{R}$ with these properties:
- Symmetry: $k(\mathbf{x_1},\mathbf{x_2}) = k(\mathbf{x_2},\mathbf{x_1}) \,\,\, \forall \mathbf{x_1},\mathbf{x_2} \in X$
- Positive definite: the kernel matrix $K$ is positive semi-definite
  - Intuitively, $k(\mathbf{x_1},\mathbf{x_2}) \geq 0$
The kernel matrix (or Gram matrix) for $n$ points of $x_1,..., x_n \in X$ is defined as:

\[\begin{split} K = XX^T = \begin{bmatrix} k(\mathbf{x_1}, \mathbf{x_1}) & \ldots & k(\mathbf{x_1}, \mathbf{x_n}) \\ \vdots & \ddots & \vdots \\ k(\mathbf{x_n}, \mathbf{x_1}) & \ldots & k(\mathbf{x_n}, \mathbf{x_n}) \end{bmatrix} \end{split}\]

Once computed ($\mathcal{O}(n^2)$), simply lookup $k(\mathbf{x_1}, \mathbf{x_2})$ for any two points
In practice, you can either supply a kernel function or precompute the kernel matrix

Linear kernel#

Input space is same as output space: $X = \mathcal{H} = \mathbb{R}^d$
Feature map $\Phi(\mathbf{x}) = \mathbf{x}$
Kernel: $ k_{linear}(\mathbf{x_i},\mathbf{x_j}) = \mathbf{x_i} \cdot \mathbf{x_j}$
Geometrically, the dot product is the projection of $\mathbf{x_j}$ on hyperplane defined by $\mathbf{x_i}$
- Becomes larger if $\mathbf{x_i}$ and $\mathbf{x_j}$ are in the same ‘direction’

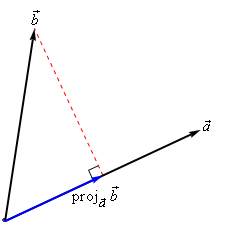
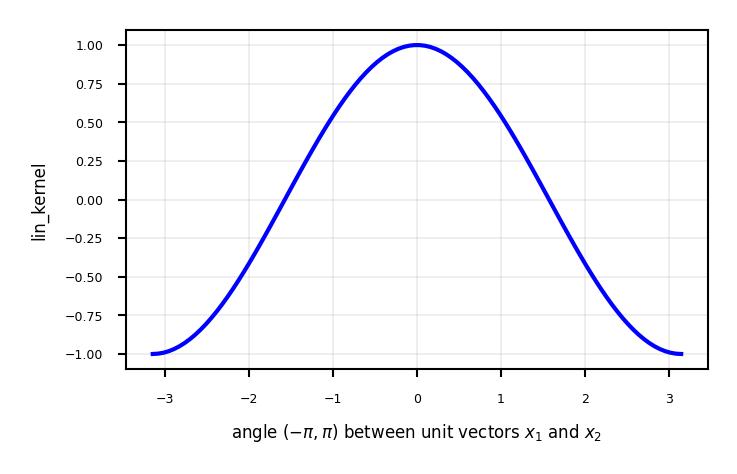
Linear kernel between point (0,1) and another unit vector an angle $a$ (in radians)
- Points with similar angles are deemed similar

_images/7e6b5b0d5f6c0873e563f36dab876a1863b557a8ce641c48fea8e1483d06c36b.png

Polynomial kernel#

If $k_1$, $k_2$ are kernels, then $\lambda . k_1$ ($\lambda \geq 0$), $k_1 + k_2$, and $k_1 . k_2$ are also kernels
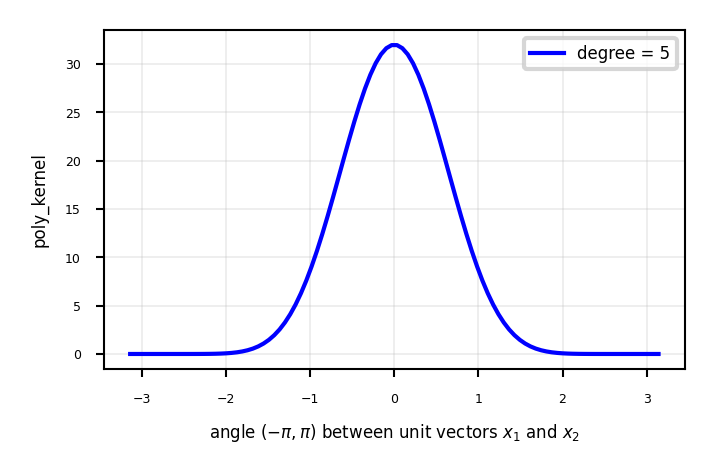
The polynomial kernel (for degree $d \in \mathbb{N}$) reproduces the polynomial feature map
- $\gamma$ is a scaling hyperparameter (default $\frac{1}{p}$)
- $c_0$ is a hyperparameter (default 1) to trade off influence of higher-order terms $$k_{poly}(\mathbf{x_1},\mathbf{x_2}) = (\gamma (\mathbf{x_1} \cdot \mathbf{x_2}) + c_0)^d$$

_images/0fa84b8add1f67c17d2bff438205681a4b31ee23ed4abbed1f4ab3740952f22d.png

RBF (Gaussian) kernel#

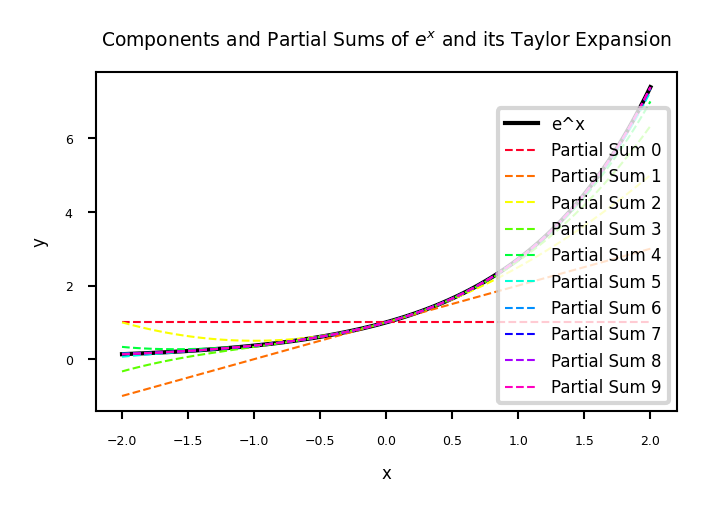
The Radial Basis Function (RBF) feature map is related to the Taylor series expansion of $e^x$ $$\Phi(x) = e^{-x^2/2\gamma^2} \Big[ 1, \sqrt{\frac{1}{1!\gamma^2}}x,\sqrt{\frac{1}{2!\gamma^4}}x^2,\sqrt{\frac{1}{3!\gamma^6}}x^3,\ldots\Big]^T$$
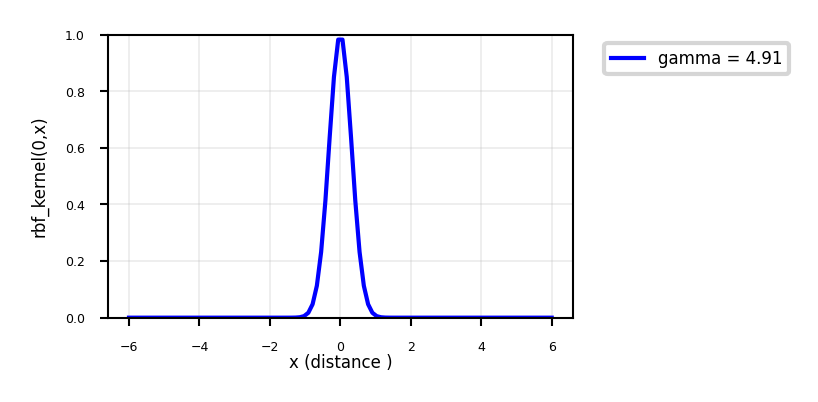
RBF (or Gaussian ) kernel with kernel width $\gamma \geq 0$:
$$k_{RBF}(\mathbf{x_1},\mathbf{x_2}) = exp(-\gamma ||\mathbf{x_1} - \mathbf{x_2}||^2)$$

_images/b1f18c203380da5ea71267509de6a221e3a7820540cc2597e05f32d5813a0fb6.png

Taylor expansion: the more we add components, the more we can approximate any function

import matplotlib.cm as cm

# Generate x values
x = np.linspace(-2, 2, 100)

# Calculate corresponding y values for e^x
y_actual = np.exp(x)

# Plot the actual function
fig, ax = plt.subplots(figsize=(5*fig_scale,3*fig_scale))
plt.plot(x, y_actual, label='e^x', linewidth=1, color='black')

# Plot the individual terms of the Taylor expansion with formulas in the legend
colors = cm.gist_rainbow(np.linspace(0, 1, 10))  # Color scheme from red to blue
for n in range(10):
    term = x**n / np.math.factorial(n)
    partial_sum = np.sum([x**i / np.math.factorial(i) for i in range(n + 1)], axis=0)
    
    # Plot partial sums with different colors
    plt.plot(x, partial_sum, label=f'Partial Sum {n}', linestyle='dashed', color=colors[n])

# Add labels and title
plt.xlabel('x')
plt.ylabel('y')
plt.title('Components and Partial Sums of $e^x$ and its Taylor Expansion')

# Display legend
plt.legend();

_images/81cdf56f49252fc0405f03dde08dfcdd8772338f9518db82e6e973977ee355a7.png

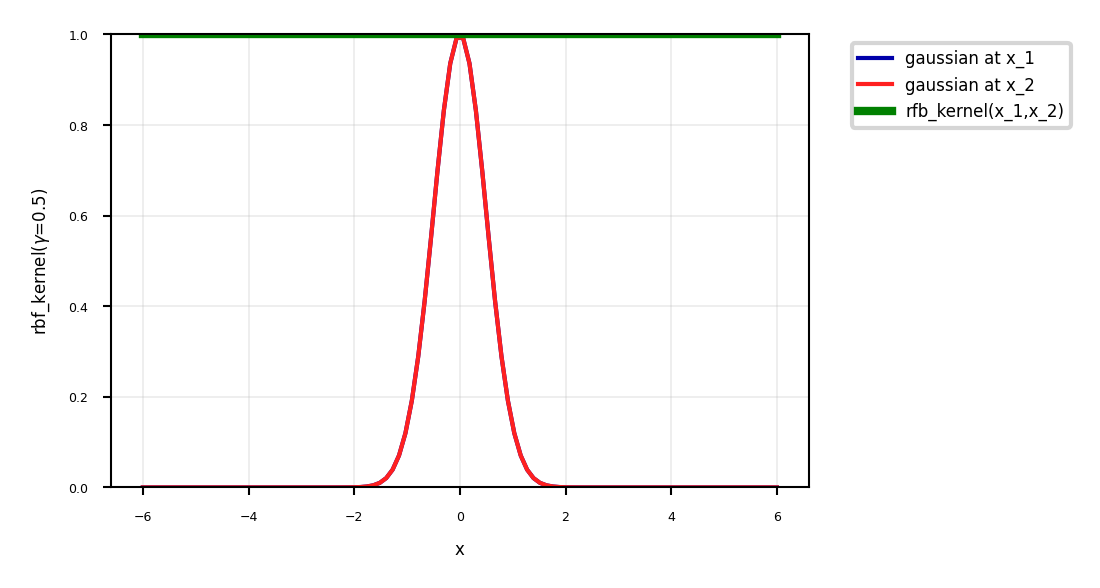
The RBF kernel $k_{RBF}(\mathbf{x_1},\mathbf{x_2}) = exp(-\gamma ||\mathbf{x_1} - \mathbf{x_2}||^2)$ does not use a dot product
- It only considers the distance between $\mathbf{x_1}$ and $\mathbf{x_2}$
- It’s a local kernel : every data point only influences data points nearby
  - linear and polynomial kernels are global : every point affects the whole space
- Similarity depends on closeness of points and kernel width
  - value goes up for closer points and wider kernels (larger overlap)

_images/5626609fe98beff7976ce4ba680ffd6105a860474a5c6e9ae93bc854536a493b.png

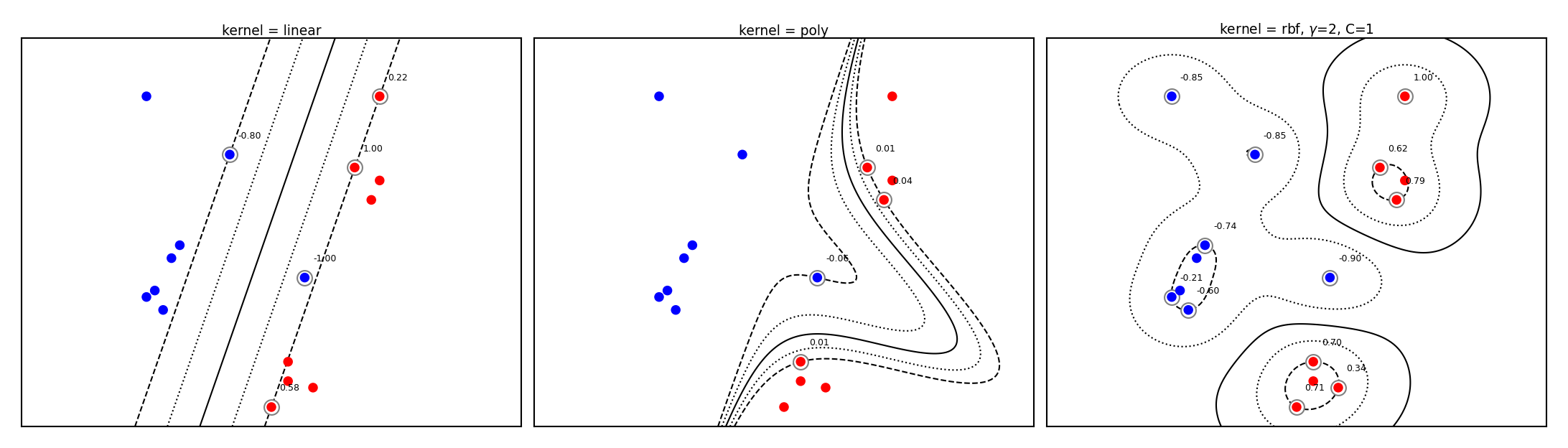
Kernelized SVMs in practice#

You can use SVMs with any kernel to learn non-linear decision boundaries

_images/00bed734aa9fdbf13e60e2cf24e53ab1bb0f7ff57c4b208828456a9ff992fc43.png

SVM with RBF kernel#

Every support vector locally influences predictions, according to kernel width ($\gamma$)
The prediction for test point $\mathbf{u}$: sum of the remaining influence of each support vector
- $f(x) = \sum_{i=1}^{l} a_i y_i k(\mathbf{x_i},\mathbf{u})$

Tuning RBF SVMs#

gamma (kernel width)
- high values cause narrow Gaussians, more support vectors, overfitting
- low values cause wide Gaussians, underfitting
C (cost of margin violations)
- high values punish margin violations, cause narrow margins, overfitting
- low values cause wider margins, more support vectors, underfitting

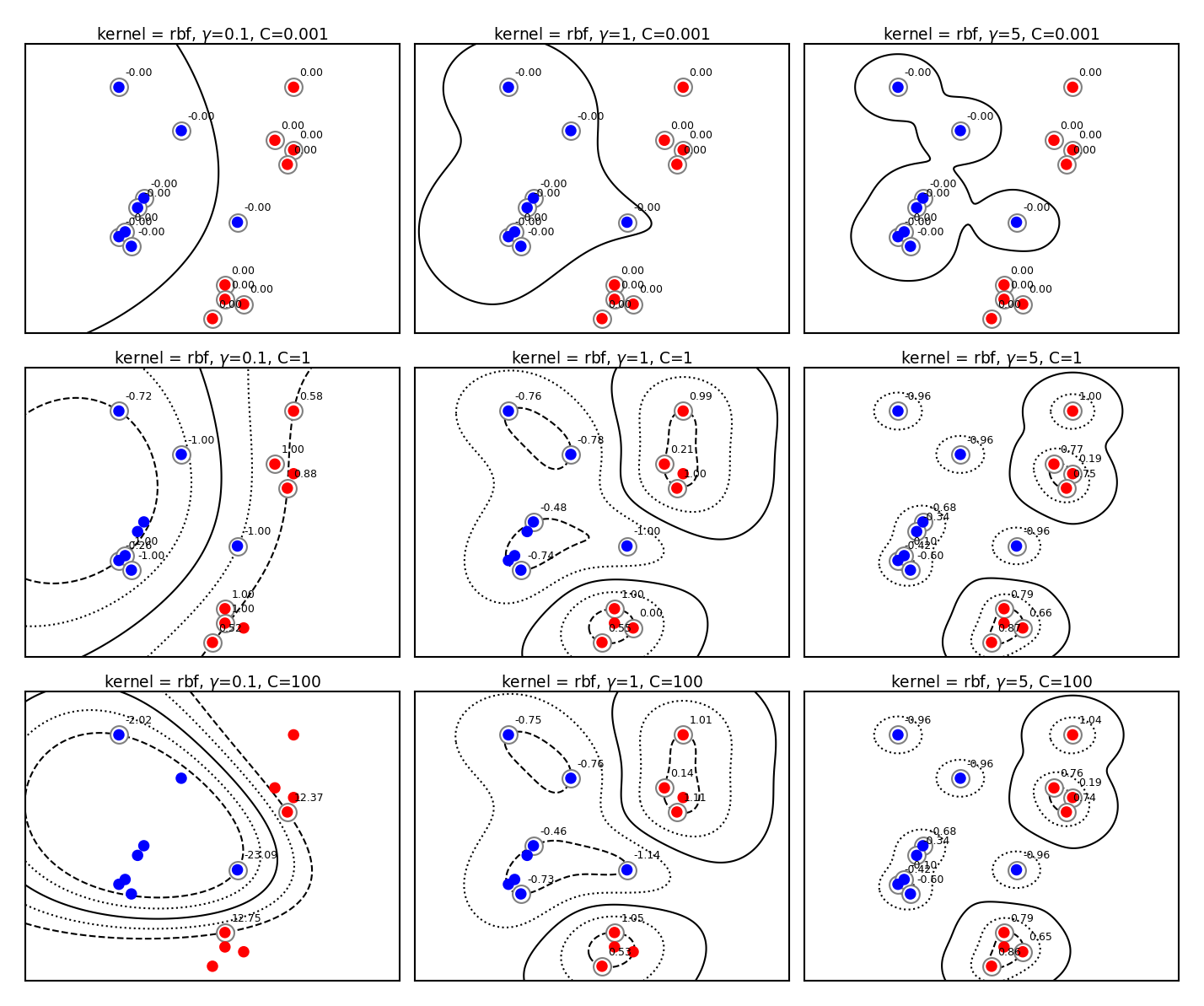
_images/88e75ca4ba0fa34d8f507fa9dce78e6f4798f1be6bfeb1fceb75710f8fb558aa.png

Kernel overview

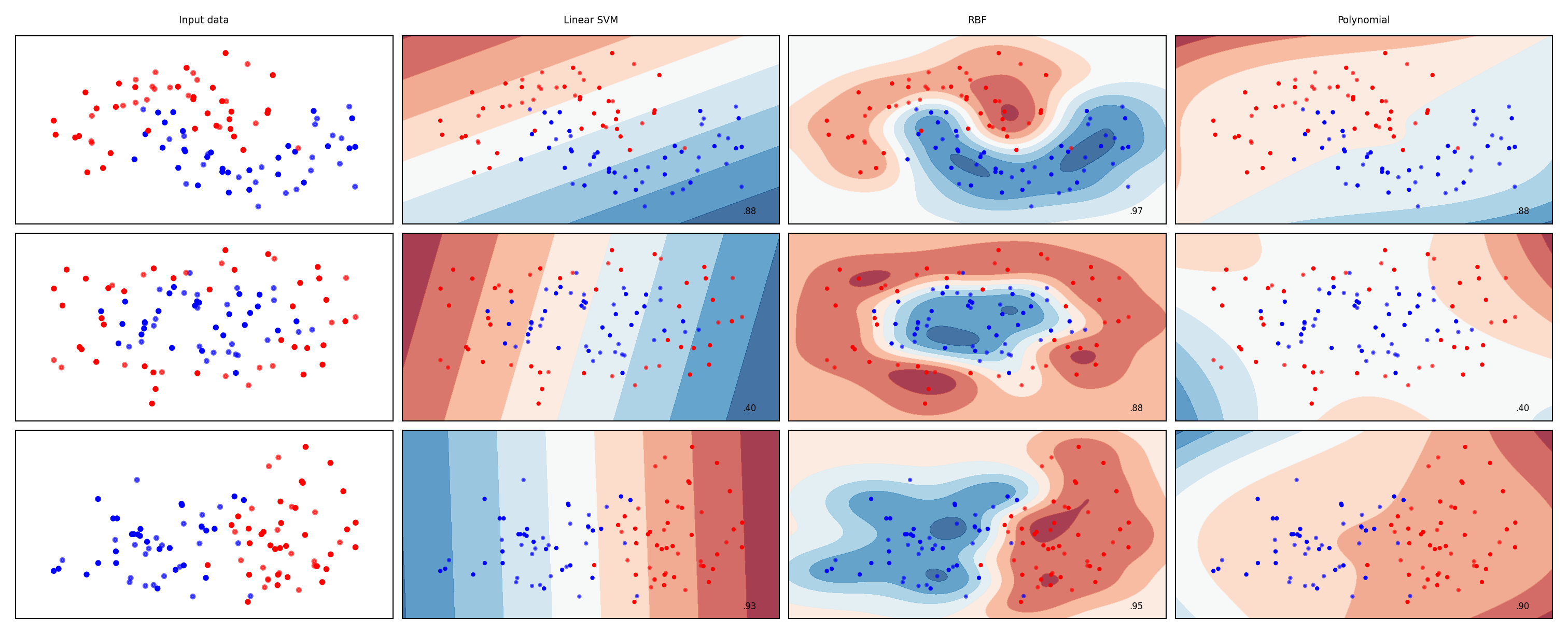
_images/7fdc31af89c5200768bf23e3102f9489f1e519fed52d693ff4de33357f612138.png

SVMs in practice#

C and gamma always need to be tuned
- Interacting regularizers. Find a good C, then finetune gamma
SVMs expect all features to be approximately on the same scale
- Data needs to be scaled beforehand
Allow to learn complex decision boundaries, even with few features
- Work well on both low- and high dimensional data
- Especially good at small, high-dimensional data
Hard to inspect, although support vectors can be inspected
In sklearn, you can use SVC for classification with a range of kernels
- SVR for regression

Other kernels#

There are many more possible kernels
If no kernel function exists, we can still precompute the kernel matrix
- All you need is some similarity measure, and you can use SVMs
Text kernels:
- Word kernels: build a bag-of-words representation of the text (e.g. TFIDF)
  - Kernel is the inner product between these vectors
- Subsequence kernels: sequences are similar if they share many sub-sequences
  - Build a kernel matrix based on pairwise similarities
Graph kernels: Same idea (e.g. find common subgraphs to measure similarity)
These days, deep learning embeddings are more frequently used

The Representer Theorem#

We can kernelize many other loss functions as well
The Representer Theorem states that if we have a loss function $\mathcal{L}'$ with
- $\mathcal{L}$ an arbitrary loss function using some function $f$ of the inputs $\mathbf{x}$
- $\mathcal{R}$ a (non-decreasing) regularization score (e.g. L1 or L2) and constant $\lambda$ $$\mathcal{\mathcal{L}'}(\mathbf{w}) = \mathcal{L}(y,f(\mathbf{x})) + \lambda \mathcal{R} (||\mathbf{w}||)$$
Then the weights $\mathbf{w}$ can be described as a linear combination of the training samples: $$\mathbf{w} = \sum_{i=1}^{n} a_i y_i f(\mathbf{x_i})$$
Note that this is exactly what we found for SVMs: $ \mathbf{w} = \sum_{i=1}^{l} a_i y_i \mathbf{\mathbf{x_i}} $
Hence, we can also kernelize Ridge regression, Logistic regression, Perceptrons, Support Vector Regression, …

Kernelized Ridge regression#

The linear Ridge regression loss (with $\mathbf{x_0}=1$): $$\mathcal{L}_{Ridge}(\mathbf{w}) = \sum_{i=0}^{n} (y_i-\mathbf{w}\mathbf{x_i})^2 + \lambda \| w \|^2$$
Filling in $\mathbf{w} = \sum_{i=1}^{n} \alpha_i y_i \mathbf{x_i}$ yields the dual formulation: $$\mathcal{L}_{Ridge}(\mathbf{w}) = \sum_{i=1}^{n} (y_i-\sum_{j=1}^{n} \alpha_j y_j \mathbf{x_i}\mathbf{x_j})^2 + \lambda \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j \mathbf{x_i}\mathbf{x_j}$$
Generalize $\mathbf{x_i}\cdot\mathbf{x_j}$ to $k(\mathbf{x_i},\mathbf{x_j})$ $$\mathcal{L}_{KernelRidge}(\mathbf{\alpha},k) = \sum_{i=1}^{n} (y_i-\sum_{j=1}^{n} \alpha_j y_j k(\mathbf{x_i},\mathbf{x_n}))^2 + \lambda \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j k(\mathbf{x_i},\mathbf{x_j})$$

Example of kernelized Ridge#

Prediction (red) is now a linear combination of kernels (blue): $y = \sum_{j=1}^{n} \alpha_j y_j k(\mathbf{x},\mathbf{x_j})$
We learn a dual coefficient for each point

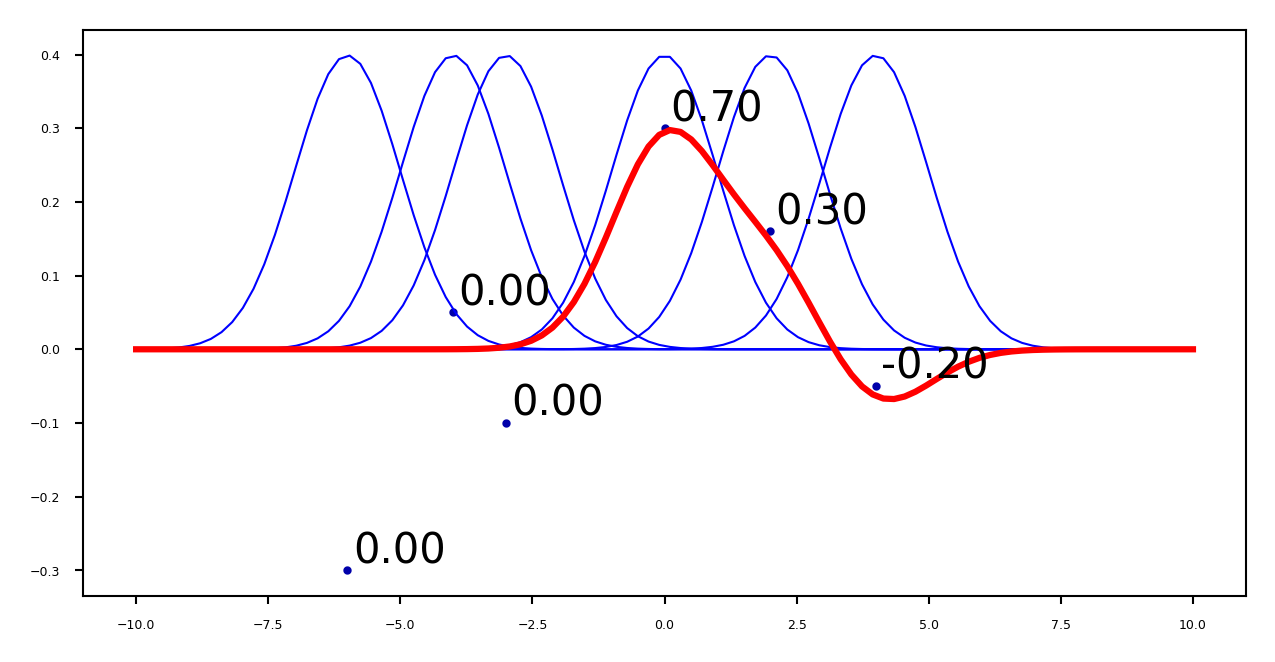
_images/9a06228ada39f756760a71294f0d1011ac40e8f07103f3b975eb82e610d8d04f.png

Fitting our regression data with KernelRidge

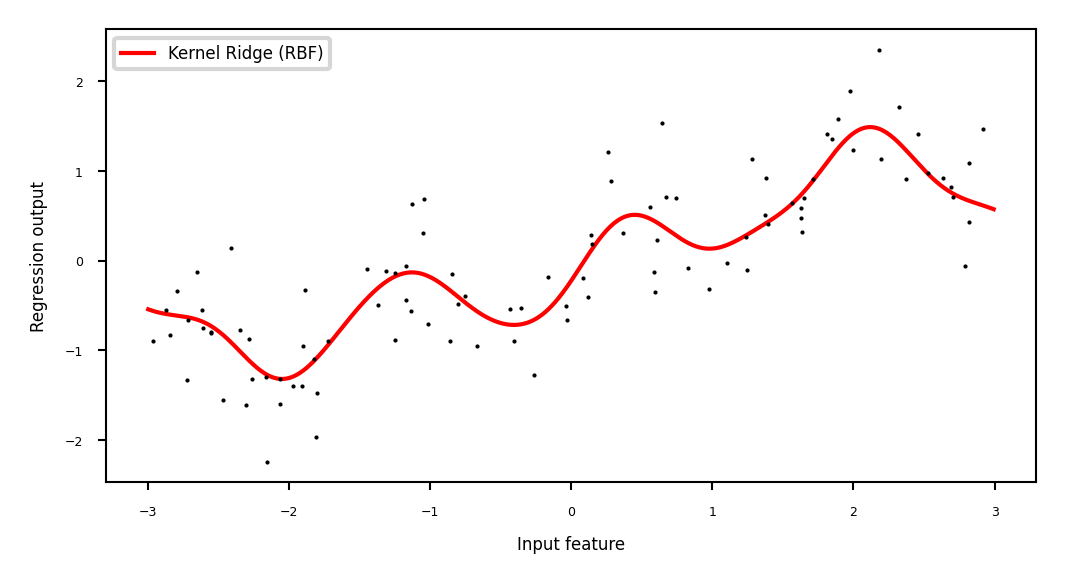
_images/d76d04122b1bc2028f74f80bd9afb76b1d724af46e4191dcf5529293ed543ead.png

Other kernelized methods#

Same procedure can be done for logistic regression
For perceptrons, $\alpha \rightarrow \alpha+1$ after every misclassification $$\mathcal{L}_{DualPerceptron}(x_i,k) = max(0,y_i \sum_{j=1}^{n} \alpha_j y_j k(\mathbf{x_j},\mathbf{x_i}))$$
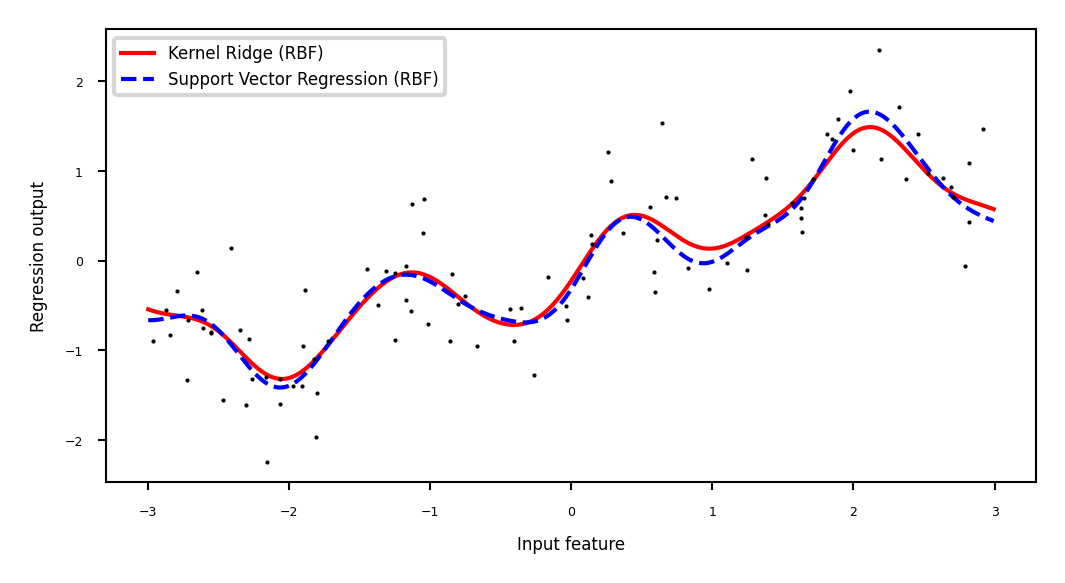
Support Vector Regression behaves similarly to Kernel Ridge

_images/d67fca93543de0e52bd35b0f7b2735db912727881fc2309e83ea360e9382eb9c.png

Summary#

Feature maps $\Phi(x)$ transform features to create a higher-dimensional space
- Allows learning non-linear functions or boundaries, but very expensive/slow
For some $\Phi(x)$, we can compute dot products without constructing this space
- Kernel trick: $k(\mathbf{x_i},\mathbf{x_j}) = \Phi(\mathbf{x_i}) \cdot \Phi(\mathbf{x_j})$
- Kernel $k$ (generalized dot product) is a measure of similarity between $\mathbf{x_i}$ and $\mathbf{x_j}$
There are many such kernels
- Polynomial kernel: $k_{poly}(\mathbf{x_1},\mathbf{x_2}) = (\gamma (\mathbf{x_1} \cdot \mathbf{x_2}) + c_0)^d$
- RBF (Gaussian) kernel: $k_{RBF}(\mathbf{x_1},\mathbf{x_2}) = exp(-\gamma ||\mathbf{x_1} - \mathbf{x_2}||^2)$
- A kernel matrix can be precomputed using any similarity measure (e.g. for text, graphs,…)
Any loss function where inputs appear only as dot products can be kernelized
- E.g. Linear SVMs: simply replace the dot product with a kernel of choice
The Representer theorem states which other loss functions can also be kernelized and how
- Ridge regression, Logistic regression, Perceptrons,…