
Advanced Deep Learning#
Mahmood Amintoosi, Spring 2024
I should mention that the original material was from Tomas Beuzen’s course.

Lecture Outline#
Lecture Learning Objectives#
Describe what an autoencoder is at a high level and what they can be useful for
Describe what a generative adversarial network is at a high level and what they can be useful for
Describe what a multi-input model is and what they can be useful for
Imports#
Show code cell source
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import torch
from torch import nn, optim
from torch.utils.data import DataLoader, TensorDataset
from torchvision import transforms, datasets, utils, models
from torchsummary import summary
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
from utils.plotting import *
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
from PIL import Image
import json
plt.style.use('ggplot')
plt.rcParams.update({'font.size': 16, 'axes.labelweight': 'bold', 'axes.grid': False})
import plotly.io as pio
pio.renderers.default = 'notebook'
1. Autoencoders#
Autoencoders (AE) are networks that are designed to reproduce their input at the output layer
They are composed of an “encoder” and “decoder”
The hidden layers of the AE are typically smaller than the input layers, such that the dimensionality of the data is reduced as it is passed through the encoder, and then expanded again in the decoder:
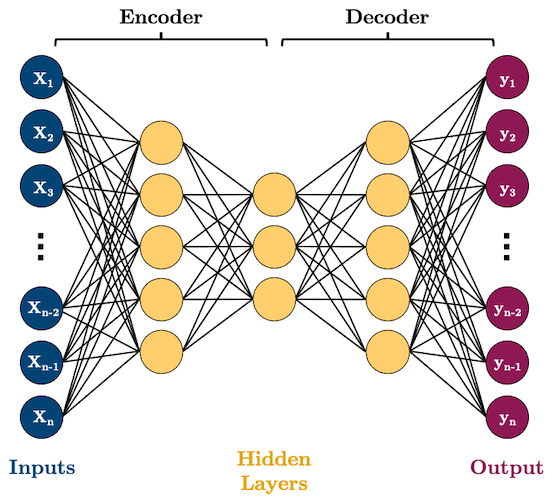
Why would you want to use such a model? As you can see, AEs perform dimensionality reduction by learning to represent your input features using fewer dimensions
That can be useful for a range of tasks but we’ll look at some specific examples below
1.1. Example 1: Dimensionality Reduction#
Here’s some synthetic data of 3 features and two classes
Can we reduce the dimensionality of this data to two features while preserving the class separation?
n_samples = 500
X, y = make_blobs(n_samples, n_features=2, centers=2, cluster_std=1, random_state=123)
X = np.concatenate((X, np.random.random((n_samples, 1))), axis=1)
X = StandardScaler().fit_transform(X)
plot_scatter3D(X, y)
We can see that
X1andX2split the data nicely, and theX3is just noiseThe question is, can an AE learn that this data can be nicely separated in just two of the three dimensions?
Let’s build a simple AE with the following neurons in each layer: 3 -> 2 -> 3:
class autoencoder(torch.nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.encoder = nn.Sequential(
nn.Linear(input_size, 2),
nn.Sigmoid()
)
self.decoder = nn.Sequential(
nn.Linear(2, input_size),
nn.Sigmoid()
)
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
BATCH_SIZE = 100
torch.manual_seed(1)
X_tensor = torch.tensor(X, dtype=torch.float32)
dataloader = DataLoader(X_tensor,
batch_size=BATCH_SIZE)
model = autoencoder(3, 2)
print(model)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters())
autoencoder(
(encoder): Sequential(
(0): Linear(in_features=3, out_features=2, bias=True)
(1): Sigmoid()
)
(decoder): Sequential(
(0): Linear(in_features=2, out_features=3, bias=True)
(1): Sigmoid()
)
)
EPOCHS = 5
for epoch in range(EPOCHS):
for batch in dataloader:
optimizer.zero_grad() # Clear gradients w.r.t. parameters
y_hat = model(batch) # Forward pass to get output
loss = criterion(y_hat, batch) # Calculate loss
loss.backward() # Getting gradients w.r.t. parameters
optimizer.step() # Update parameters
We only care about the encoder now, does it represent our data nicely in reduced dimensions?
model.eval()
print(f"Original X shape = {X_tensor.shape}")
X_encoded = model.encoder(X_tensor)
print(f" Encoded X shape = {X_encoded.shape}")
Original X shape = torch.Size([500, 3])
Encoded X shape = torch.Size([500, 2])
plot_scatter2D(X_encoded, y)
What did we just do? We used an AE to effectively reduce the number of features in our data
This is very similar to concepts of unsupervised learning and clustering that you’ll discuss in DSCI 563.
1.2. Example 2: Image Denoising#
Okay, let’s do something more interesting
We saw above that AEs can be useful feature reducers (i.e., they can remove unimportant features from our data)
This also applies to images and it’s a fun application to de-noise images!
Take a look at these images of 8’s from the MNIST dataset, I’m going to mess them up by adding some noise to them:
BATCH_SIZE = 32
# Download data
transform = transforms.Compose([transforms.ToTensor()])
trainset = datasets.MNIST('../../data/', download=True, train=True, transform=transform)
idx = trainset.targets == 8 # let's only work with the number 8
trainset.targets = trainset.targets[idx]
trainset.data = trainset.data[idx]
trainloader = torch.utils.data.DataLoader(trainset, batch_size=BATCH_SIZE, shuffle=True)
# Sample plot
X, y = next(iter(trainloader))
noise = 0.5
plot_eights(X, noise)
Show code cell output
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Failed to download (trying next):
<urlopen error [SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed: certificate has expired (_ssl.c:1007)>
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-images-idx3-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-images-idx3-ubyte.gz to ../../data/MNIST\raw\train-images-idx3-ubyte.gz
100%|██████████| 9.91M/9.91M [00:10<00:00, 945kB/s]
Extracting ../../data/MNIST\raw\train-images-idx3-ubyte.gz to ../../data/MNIST\raw
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Failed to download (trying next):
<urlopen error [SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed: certificate has expired (_ssl.c:1007)>
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-labels-idx1-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/train-labels-idx1-ubyte.gz to ../../data/MNIST\raw\train-labels-idx1-ubyte.gz
100%|██████████| 28.9k/28.9k [00:00<00:00, 159kB/s]
Extracting ../../data/MNIST\raw\train-labels-idx1-ubyte.gz to ../../data/MNIST\raw
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Failed to download (trying next):
<urlopen error [SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed: certificate has expired (_ssl.c:1007)>
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-images-idx3-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-images-idx3-ubyte.gz to ../../data/MNIST\raw\t10k-images-idx3-ubyte.gz
100%|██████████| 1.65M/1.65M [00:01<00:00, 1.18MB/s]
Extracting ../../data/MNIST\raw\t10k-images-idx3-ubyte.gz to ../../data/MNIST\raw
Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz
Failed to download (trying next):
<urlopen error [SSL: CERTIFICATE_VERIFY_FAILED] certificate verify failed: certificate has expired (_ssl.c:1007)>
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-labels-idx1-ubyte.gz
Downloading https://ossci-datasets.s3.amazonaws.com/mnist/t10k-labels-idx1-ubyte.gz to ../../data/MNIST\raw\t10k-labels-idx1-ubyte.gz
100%|██████████| 4.54k/4.54k [00:00<00:00, 4.54MB/s]
Extracting ../../data/MNIST\raw\t10k-labels-idx1-ubyte.gz to ../../data/MNIST\raw
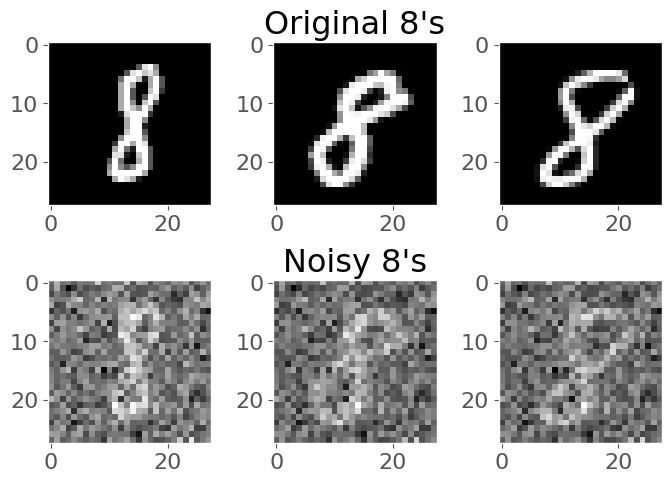
Can we train an AE to get rid of that noise and reconstruct the original 8’s? Let’s give it a try!
I’m going to use convolutional layers in my AE now as we are dealing with images
We’ll use
Conv2D()layers to compress our images into a reduced dimensonality, and then we need to “upsample” it back to the original sizeOne ingredient you’ll need to know to do this is “transposed convolutional layers”. These are just like “convolutional layers” but for the purpose of “upsampling” (increasing the size of) our data. Rather than simply expanding the size of our data and interpolating, we use
nn.ConvTranspose2d()layers to help us learn how to best upsample our data:
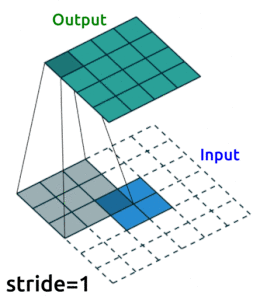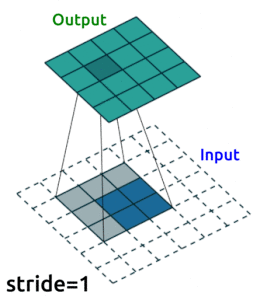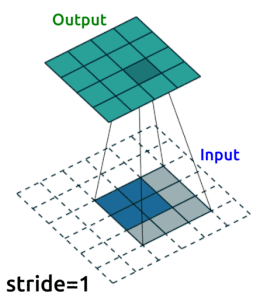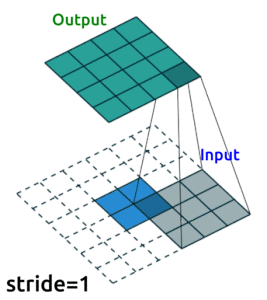
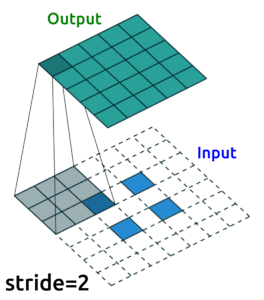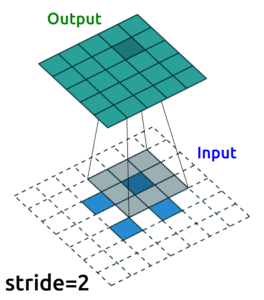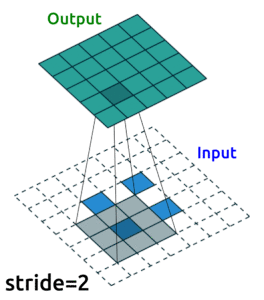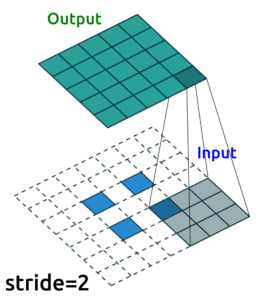
Source: modified from A guide to convolution arithmetic for deep learning, Vincent Dumoulin (2018)
See Transposed Convolution in appendices.
def conv_block(input_channels, output_channels):
return nn.Sequential(
nn.Conv2d(input_channels, output_channels, 3, padding=1),
nn.ReLU(),
nn.MaxPool2d(2) # reduce x-y dims by two; window and stride of 2
)
def deconv_block(input_channels, output_channels, kernel_size):
return nn.Sequential(
nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride=2),
nn.ReLU()
)
class autoencoder(torch.nn.Module):
def __init__(self):
super().__init__()
self.encoder = nn.Sequential(
conv_block(1, 32),
conv_block(32, 16),
conv_block(16, 8)
)
self.decoder = nn.Sequential(
deconv_block(8, 8, 3),
deconv_block(8, 16, 2),
deconv_block(16, 32, 2),
nn.Conv2d(32, 1, 3, padding=1) # final conv layer to decrease channel back to 1
)
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
x = torch.sigmoid(x) # get pixels between 0 and 1
return x
So we want to train our model to remove that noise I added
Generally speaking, the idea is that the model learns what pixel values are important, we are reducing the dimensionality of the imaages, so our model must learn only the crucial information (i.e., not the noise) needed to reproduce the image
Right now, our model probably produces gibberish because it isn’t trained:
model = autoencoder()
input_8 = X[:1, :1, :, :]
output_8 = model(input_8)
plot_eight_pair(input_8, output_8)
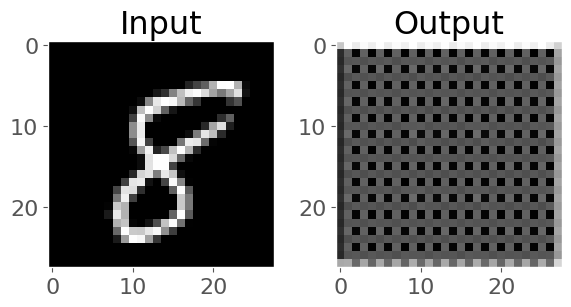
How do we train it?
Well we feed in a noisy image, compare it to the non-noisy version, and let the network learn how to make that happen
We want the value of the predicted pixels to be as close as possible to the real pixel values, so we’ll use
MSELoss()as our loss function:
%%time
EPOCHS = 20
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters())
img_list = []
for epoch in range(EPOCHS):
losses = 0
for batch, _ in trainloader:
noisy_batch = batch + noise * torch.randn(*batch.shape)
noisy_batch = torch.clip(noisy_batch, 0.0, 1.0)
optimizer.zero_grad()
y_hat = model(noisy_batch)
loss = criterion(y_hat, batch)
loss.backward()
optimizer.step()
losses += loss.item()
print(f"epoch: {epoch + 1}, loss: {losses / len(trainloader):.4f}")
# Save example results each epoch so we can see what's going on
with torch.no_grad():
noisy_8 = noisy_batch[:1, :1, :, :]
model_8 = model(input_8)
real_8 = batch[:1, :1, :, :]
img_list.append(utils.make_grid([noisy_8[0], model_8[0], real_8[0]], padding=1))
epoch: 1, loss: 0.1079
epoch: 2, loss: 0.0576
epoch: 3, loss: 0.0477
epoch: 4, loss: 0.0444
epoch: 5, loss: 0.0422
epoch: 6, loss: 0.0406
epoch: 7, loss: 0.0393
epoch: 8, loss: 0.0382
epoch: 9, loss: 0.0371
epoch: 10, loss: 0.0362
epoch: 11, loss: 0.0355
epoch: 12, loss: 0.0348
epoch: 13, loss: 0.0341
epoch: 14, loss: 0.0336
epoch: 15, loss: 0.0332
epoch: 16, loss: 0.0326
epoch: 17, loss: 0.0324
epoch: 18, loss: 0.0320
epoch: 19, loss: 0.0317
epoch: 20, loss: 0.0315
CPU times: total: 7min 47s
Wall time: 2min 33s
%%capture
fig, ax = plt.subplots(1, 1, figsize=(8, 5))
ax.set_title("Input Prediction Actual")
ims = [[plt.imshow(np.transpose(i, (1,2,0)), animated=True)] for i in img_list]
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)
# ani.save('eights.gif', writer='imagemagick', fps=2)
# HTML(ani.to_jshtml()) # run this in a new cell to produce the below animation
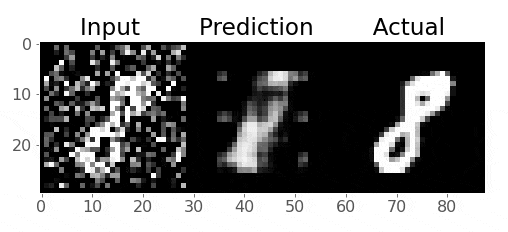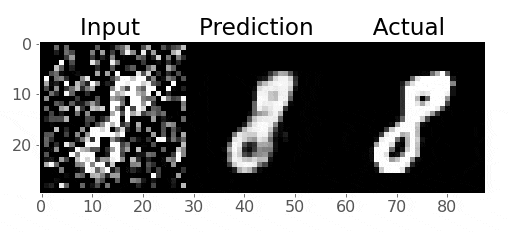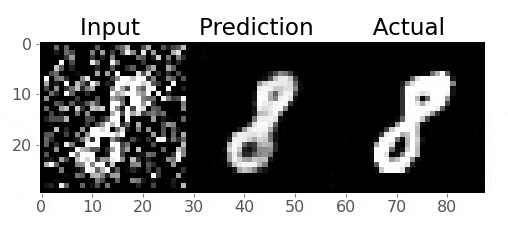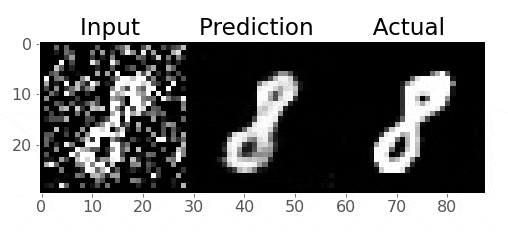
Pretty cool!
2. Generative Adversarial Networks (GANs)#
2.1. What are GANs?#
GANs were invented in 2014 by Ian Goodfellow and colleagues
GANs are pretty complex but they are just so cool so I wanted to talk about them briefly
The goal of a GAN is to develop a model that can generate realistic “fake” data, like the face below
If you look closely, you’ll notice that some things don’t look quite right, like the glasses…

GANs are mostly used to generate imagery at the moment so I’ll speak about them in that context
The “adversarial” comes from the fact that we actually have two networks “battling” each other:
The “Generator”: takes some noise (like Gaussian noise) as input and generates “fake” data (like an image)
The “Discriminator”: takes in real and fake data from the generator and attempts to classify it as “real” or “fake”
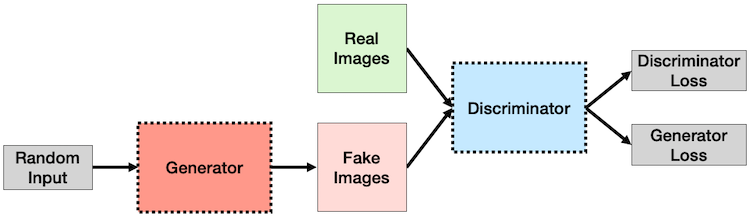
An analogy always helps
Think of the “Generator” as a new counterfeit artist trying to produce realistic-looking famous artworks to sell

The “Discriminator” is an art-critic, trying to determine if a piece of art is “real” or “fake”
At first, the “Generator” produces poor art-replicas which the “Discriminator” can easily tell are fake

But over time, the “Generator” learns ways to produce art that fools the “Discriminator”
Eventually, the “Generator” gets so good, that the “Discriminator” can’t tell if a piece of art is real or fake - the “Generator” is now able to generate realistic fake artwork! Money, money, money!

GANs are mostly used to generate imagery at the moment so I’ll focus on that
Training a GAN really happens in two iterative phases:
Train the Discriminator:
Generate some fake images with the generator
Show the discriminator real images and fake images and get it to classify them correctly (a simple binary classification problem)
Train the Generator:
Generate fake images with the generator but label them as “real”
At first, the discriminator will easily identify the “fake” images as “fake” (it’s already been trained a little bit to do this)
This means the generator will have a large loss (the discriminator predicted the images as “fake” but the label is “real”)
We use this loss to update the generator’s weights. Next time around, the loss will be less, because the generator will produce some images that the discriminator thinks are real.
Repeat!
Additional Resources:#
How to Develop a 1D Generative Adversarial Network From Scratch in Keras
Colab GAN-01, Exercise: Convert TF2PyTorch
Enough talk, let’s code it up!
2.2. An Example: Generating Bitmojis#
I’m going to use our favourite bitmoji dataset to try and develop a GAN (this may or may not go well):
# Training Parameters
IMAGE_SIZE = 64
BATCH_SIZE = 64
LATENT_SIZE = 100
NUM_EPOCHS = 200 # we often need a lot of epochs to train GANs
LR = 0.0008
IMAGE_DIR = "data/bitmoji_rgb/train/"
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(f"Using device: {device.type}")
# Transforms
data_transforms = transforms.Compose([transforms.Resize(IMAGE_SIZE), transforms.ToTensor()])
# Loader
bitmoji_dataset = datasets.ImageFolder(root=IMAGE_DIR, transform=data_transforms)
bitmoji_loader = torch.utils.data.DataLoader(bitmoji_dataset, batch_size=BATCH_SIZE, shuffle=True)
Using device: cuda
I’m going to base my architecture off the one in the original Deep Convolutional (DCGAN) paper
Here’s the generator (the disciminator is the inverse of this):
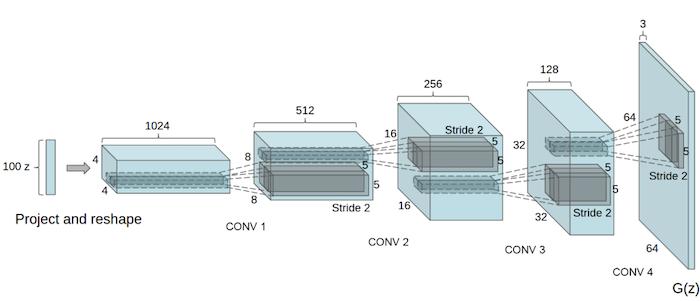
This is pretty complex stuff, but amazingly, we know what all of this is going to mean
Let’s create the “Generator” first:
def convtrans_block(in_channels, out_channels, kernel_size, stride, padding):
return nn.Sequential(
nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride, padding, bias=False),
nn.BatchNorm2d(out_channels),
nn.ReLU()
)
class Generator(nn.Module):
def __init__(self, LATENT_SIZE):
super().__init__()
self.main = nn.Sequential(
convtrans_block(LATENT_SIZE, 512, 4, stride=1, padding=0),
convtrans_block(512, 256, 4, stride=2, padding=1),
convtrans_block(256, 128, 4, stride=2, padding=1),
convtrans_block(128, 64, 4, stride=2, padding=1),
convtrans_block(64, 3, 4, stride=2, padding=1),
nn.Tanh()
)
def forward(self, x):
return self.main(x)
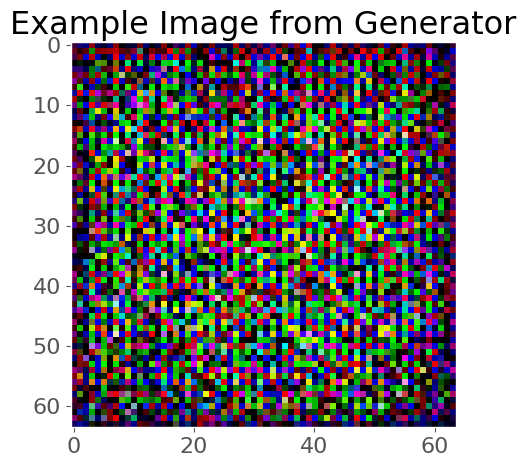
We should be able to pass some noise to our generator and it will spit out an image (probably not a good one yet, as we haven’t trained!):
generator = Generator(LATENT_SIZE)
example_noise = torch.randn(1, LATENT_SIZE, 1, 1)
fake = generator(example_noise).squeeze().detach()
plt.figure(figsize=(5, 5))
plt.title("Example Image from Generator")
plt.imshow(np.transpose(fake, (1, 2, 0)));
Create discriminator
def conv_block(in_channels, out_channels, kernel_size, stride, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding, bias=False),
nn.BatchNorm2d(out_channels),
nn.LeakyReLU(0.2, True)
)
class Discriminator(nn.Module):
def __init__(self):
super().__init__()
self.main = nn.Sequential(
nn.Conv2d(3, 64, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, True),
conv_block(64, 128, 4, 2, 1),
conv_block(128, 256, 4, 2, 1),
conv_block(256, 512, 4, 2, 1),
nn.Conv2d(512, 1, 4, 1, 0, bias=False),
nn.Sigmoid()
)
def forward(self, x):
return self.main(x)
Let’s make sure our discriminator is able to make a prediction:
discriminator = Discriminator()
fake = generator(example_noise)
discriminator(fake).item()
0.48948991298675537
Okay, we’re almost ready to train, the DCGAN paper recommends initializing the GAN with values from a normal distribution
I’ll talk more about this later, for now, I’m just going to run this function:
def weights_init(m):
if isinstance(m, (nn.Conv2d, nn.ConvTranspose2d)):
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif isinstance(m, nn.BatchNorm2d):
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
generator = Generator(LATENT_SIZE)
generator.apply(weights_init)
generator.to(device)
discriminator = Discriminator()
discriminator.apply(weights_init)
discriminator.to(device)
Okay, we’re ready to train
Our loss functions will be
BCEWithLogitsLoss()- remember, the discriminator is just a binary classification networkHowever, because we train the generator and discriminator separately, we’ll need two optimizers:
criterion = nn.BCELoss()
optimizerG = optim.Adam(generator.parameters(), lr=LR, betas=(0.5, 0.999))
optimizerD = optim.Adam(discriminator.parameters(), lr=LR, betas=(0.5, 0.999))
fixed_noise = torch.randn(BATCH_SIZE, LATENT_SIZE, 1, 1, device=device) # Fixed noise vector we'll use to track image generation evolution
I’ve meticulously commented each line in the following training loop, hopefully it’s not too hard to follow!
%%time
# Lists to keep track of progress
img_list = []
gen_losses = []
dis_losses = []
ITERS = 0
print("Begin training...")
for epoch in range(NUM_EPOCHS):
for real_batch, _ in bitmoji_loader:
### STEP 1: train discriminator
# Train with real data
discriminator.zero_grad()
real_batch = real_batch.to(device)
real_labels = torch.ones((real_batch.shape[0],), dtype=torch.float, device=device) # Real labels
output = discriminator(real_batch).view(-1) # Forward pass real batch through discriminator
loss_real = criterion(output, real_labels) # Calculate discriminator loss on real batch
loss_real.backward() # Calculate gradients for discriminator with backward pass
D_real = output.mean().item() # Avg. D output on real batch
# Train with fake data
noise = torch.randn(real_batch.shape[0], LATENT_SIZE, 1, 1, device=device) # Generate some noise to feed to generator
fake_batch = generator(noise) # Generate fake images with generator using the noise vector
fake_labels = torch.zeros_like(real_labels) # Fake labels
output = discriminator(fake_batch.detach()).view(-1) # Forward pass fake batch through discriminator (detach the generator though! we don't want to backprop through it)
loss_fake = criterion(output, fake_labels) # Calculate discriminator loss on real batch
loss_fake.backward() # Calculate gradients for discriminator with backward pass
D_fake = output.mean().item() # Avg. D output on fake batch
# Update discriminator weights and store loss
optimizerD.step()
loss_dis = loss_real + loss_fake
### STEP 2: train generator
generator.zero_grad()
output = discriminator(fake_batch).view(-1) # Forward pass fake batch through updated discriminator
loss_gen = criterion(output, real_labels) # Calculate generator loss on fake batch
loss_gen.backward() # Calculate gradients for generator with backward pass
# Update generator weights and store loss
optimizerG.step()
# Metadata
gen_losses.append(loss_gen.item())
dis_losses.append(loss_dis.item())
if ITERS % 50 == 0:
print(f"Epoch ({epoch + 1}/{NUM_EPOCHS})",
f"Iteration ({ITERS + 1})",
f"Loss_G: {loss_gen.item():.4f}",
f"Loss_D: {loss_dis.item():.4f}",
f"D_real: {D_real:.4f}", # this should start around 1 and go down to 0.5 over time
f"D_fake: {D_fake:.4f}") # this should start around 0 and go up to 0.5 over time
ITERS += 1
### Store loss and track image evolution
if epoch % 2 == 0:
with torch.no_grad():
fake_images = generator(fixed_noise).detach().cpu()
img_list.append(utils.make_grid(fake_images, nrow=4, normalize=True))
print("Finished training!")
Show code cell output
Begin training...
Epoch (1/200) Iteration (1) Loss_G: 14.9377 Loss_D: 1.9841 D_real: 0.4098 D_fake: 0.5358
Epoch (2/200) Iteration (51) Loss_G: 38.9919 Loss_D: 0.0000 D_real: 1.0000 D_fake: 0.0000
Epoch (4/200) Iteration (101) Loss_G: 38.1705 Loss_D: 0.0000 D_real: 1.0000 D_fake: 0.0000
Epoch (6/200) Iteration (151) Loss_G: 0.0000 Loss_D: 100.0002 D_real: 0.9998 D_fake: 1.0000
Epoch (8/200) Iteration (201) Loss_G: 5.3094 Loss_D: 8.3992 D_real: 0.0282 D_fake: 0.0029
Epoch (10/200) Iteration (251) Loss_G: 4.0712 Loss_D: 0.2853 D_real: 0.8592 D_fake: 0.1106
Epoch (12/200) Iteration (301) Loss_G: 3.6460 Loss_D: 1.3744 D_real: 0.9850 D_fake: 0.5297
Epoch (13/200) Iteration (351) Loss_G: 3.9092 Loss_D: 0.1415 D_real: 0.9454 D_fake: 0.0783
Epoch (15/200) Iteration (401) Loss_G: 4.7152 Loss_D: 0.2218 D_real: 0.9721 D_fake: 0.1580
Epoch (17/200) Iteration (451) Loss_G: 0.9062 Loss_D: 0.8309 D_real: 0.5063 D_fake: 0.0222
Epoch (19/200) Iteration (501) Loss_G: 5.2779 Loss_D: 0.4013 D_real: 0.9171 D_fake: 0.2396
Epoch (21/200) Iteration (551) Loss_G: 5.5213 Loss_D: 1.4228 D_real: 0.3931 D_fake: 0.0028
Epoch (23/200) Iteration (601) Loss_G: 3.1179 Loss_D: 0.1830 D_real: 0.9256 D_fake: 0.0816
Epoch (25/200) Iteration (651) Loss_G: 2.5187 Loss_D: 0.6514 D_real: 0.9901 D_fake: 0.4461
Epoch (26/200) Iteration (701) Loss_G: 3.5017 Loss_D: 0.3327 D_real: 0.8468 D_fake: 0.1400
Epoch (28/200) Iteration (751) Loss_G: 4.5595 Loss_D: 1.6357 D_real: 0.8126 D_fake: 0.6492
Epoch (30/200) Iteration (801) Loss_G: 3.4527 Loss_D: 0.7699 D_real: 0.7677 D_fake: 0.3249
Epoch (32/200) Iteration (851) Loss_G: 1.9626 Loss_D: 1.1116 D_real: 0.5971 D_fake: 0.2841
Epoch (34/200) Iteration (901) Loss_G: 2.8130 Loss_D: 1.3043 D_real: 0.7158 D_fake: 0.4410
Epoch (36/200) Iteration (951) Loss_G: 2.0214 Loss_D: 0.5292 D_real: 0.7780 D_fake: 0.1677
Epoch (38/200) Iteration (1001) Loss_G: 2.8038 Loss_D: 0.8583 D_real: 0.8001 D_fake: 0.4141
Epoch (39/200) Iteration (1051) Loss_G: 1.9742 Loss_D: 0.9099 D_real: 0.5702 D_fake: 0.1579
Epoch (41/200) Iteration (1101) Loss_G: 3.3688 Loss_D: 0.8229 D_real: 0.8322 D_fake: 0.3718
Epoch (43/200) Iteration (1151) Loss_G: 4.2120 Loss_D: 0.4097 D_real: 0.8957 D_fake: 0.2336
Epoch (45/200) Iteration (1201) Loss_G: 2.0499 Loss_D: 0.9265 D_real: 0.5755 D_fake: 0.2075
Epoch (47/200) Iteration (1251) Loss_G: 2.7327 Loss_D: 0.8988 D_real: 0.6119 D_fake: 0.2007
Epoch (49/200) Iteration (1301) Loss_G: 5.6085 Loss_D: 0.6461 D_real: 0.8225 D_fake: 0.3132
Epoch (51/200) Iteration (1351) Loss_G: 3.6084 Loss_D: 0.5646 D_real: 0.7856 D_fake: 0.2097
Epoch (52/200) Iteration (1401) Loss_G: 4.3127 Loss_D: 0.6438 D_real: 0.9593 D_fake: 0.3363
Epoch (54/200) Iteration (1451) Loss_G: 5.8637 Loss_D: 1.1297 D_real: 0.9374 D_fake: 0.5541
Epoch (56/200) Iteration (1501) Loss_G: 3.4013 Loss_D: 1.8468 D_real: 0.2222 D_fake: 0.0068
Epoch (58/200) Iteration (1551) Loss_G: 2.9591 Loss_D: 0.2460 D_real: 0.8968 D_fake: 0.1145
Epoch (60/200) Iteration (1601) Loss_G: 5.0026 Loss_D: 0.6102 D_real: 0.6803 D_fake: 0.0942
Epoch (62/200) Iteration (1651) Loss_G: 3.2022 Loss_D: 0.5062 D_real: 0.6923 D_fake: 0.0623
Epoch (63/200) Iteration (1701) Loss_G: 3.5346 Loss_D: 0.2534 D_real: 0.8271 D_fake: 0.0447
Epoch (65/200) Iteration (1751) Loss_G: 3.7430 Loss_D: 1.3626 D_real: 0.3801 D_fake: 0.0274
Epoch (67/200) Iteration (1801) Loss_G: 5.1671 Loss_D: 0.4117 D_real: 0.9060 D_fake: 0.2296
Epoch (69/200) Iteration (1851) Loss_G: 6.1744 Loss_D: 0.7611 D_real: 0.9792 D_fake: 0.4512
Epoch (71/200) Iteration (1901) Loss_G: 4.9117 Loss_D: 0.4382 D_real: 0.8249 D_fake: 0.1636
Epoch (73/200) Iteration (1951) Loss_G: 4.2309 Loss_D: 0.3508 D_real: 0.9784 D_fake: 0.2387
Epoch (75/200) Iteration (2001) Loss_G: 4.1182 Loss_D: 0.3164 D_real: 0.8263 D_fake: 0.0802
Epoch (76/200) Iteration (2051) Loss_G: 5.0597 Loss_D: 0.4086 D_real: 0.9635 D_fake: 0.2508
Epoch (78/200) Iteration (2101) Loss_G: 4.1649 Loss_D: 0.4443 D_real: 0.7570 D_fake: 0.0893
Epoch (80/200) Iteration (2151) Loss_G: 4.6576 Loss_D: 0.2053 D_real: 0.9548 D_fake: 0.1276
Epoch (82/200) Iteration (2201) Loss_G: 6.7406 Loss_D: 0.2307 D_real: 0.9634 D_fake: 0.1456
Epoch (84/200) Iteration (2251) Loss_G: 7.5099 Loss_D: 0.6066 D_real: 0.9156 D_fake: 0.3412
Epoch (86/200) Iteration (2301) Loss_G: 3.9546 Loss_D: 0.6399 D_real: 0.7980 D_fake: 0.2326
Epoch (88/200) Iteration (2351) Loss_G: 3.5848 Loss_D: 0.4493 D_real: 0.7836 D_fake: 0.1234
Epoch (89/200) Iteration (2401) Loss_G: 3.9403 Loss_D: 0.4114 D_real: 0.8133 D_fake: 0.1241
Epoch (91/200) Iteration (2451) Loss_G: 2.7614 Loss_D: 0.4381 D_real: 0.7503 D_fake: 0.0808
Epoch (93/200) Iteration (2501) Loss_G: 1.7395 Loss_D: 0.8307 D_real: 0.5928 D_fake: 0.0593
Epoch (95/200) Iteration (2551) Loss_G: 4.6953 Loss_D: 0.2640 D_real: 0.8825 D_fake: 0.0905
Epoch (97/200) Iteration (2601) Loss_G: 3.0785 Loss_D: 0.4684 D_real: 0.7797 D_fake: 0.1265
Epoch (99/200) Iteration (2651) Loss_G: 4.3978 Loss_D: 0.3214 D_real: 0.8629 D_fake: 0.0651
Epoch (101/200) Iteration (2701) Loss_G: 2.9100 Loss_D: 0.2554 D_real: 0.8240 D_fake: 0.0315
Epoch (102/200) Iteration (2751) Loss_G: 5.1647 Loss_D: 0.3032 D_real: 0.8890 D_fake: 0.1216
Epoch (104/200) Iteration (2801) Loss_G: 3.1631 Loss_D: 0.3933 D_real: 0.7714 D_fake: 0.0290
Epoch (106/200) Iteration (2851) Loss_G: 6.2199 Loss_D: 0.0934 D_real: 0.9674 D_fake: 0.0535
Epoch (108/200) Iteration (2901) Loss_G: 6.5708 Loss_D: 1.2014 D_real: 0.8124 D_fake: 0.3881
Epoch (110/200) Iteration (2951) Loss_G: 5.4796 Loss_D: 0.1705 D_real: 0.8997 D_fake: 0.0482
Epoch (112/200) Iteration (3001) Loss_G: 5.5784 Loss_D: 0.1898 D_real: 0.9586 D_fake: 0.1124
Epoch (113/200) Iteration (3051) Loss_G: 4.6796 Loss_D: 0.0908 D_real: 0.9746 D_fake: 0.0594
Epoch (115/200) Iteration (3101) Loss_G: 5.5262 Loss_D: 0.3667 D_real: 0.9191 D_fake: 0.1852
Epoch (117/200) Iteration (3151) Loss_G: 5.1491 Loss_D: 0.1559 D_real: 0.9526 D_fake: 0.0939
Epoch (119/200) Iteration (3201) Loss_G: 4.8784 Loss_D: 0.1585 D_real: 0.9205 D_fake: 0.0563
Epoch (121/200) Iteration (3251) Loss_G: 4.2500 Loss_D: 0.1600 D_real: 0.9018 D_fake: 0.0380
Epoch (123/200) Iteration (3301) Loss_G: 5.6614 Loss_D: 0.1135 D_real: 0.9599 D_fake: 0.0591
Epoch (125/200) Iteration (3351) Loss_G: 4.8153 Loss_D: 0.1346 D_real: 0.9599 D_fake: 0.0667
Epoch (126/200) Iteration (3401) Loss_G: 5.2183 Loss_D: 0.1269 D_real: 0.9523 D_fake: 0.0637
Epoch (128/200) Iteration (3451) Loss_G: 4.7515 Loss_D: 0.4221 D_real: 0.8098 D_fake: 0.0871
Epoch (130/200) Iteration (3501) Loss_G: 4.9045 Loss_D: 0.0998 D_real: 0.9624 D_fake: 0.0554
Epoch (132/200) Iteration (3551) Loss_G: 4.6365 Loss_D: 0.0642 D_real: 0.9753 D_fake: 0.0360
Epoch (134/200) Iteration (3601) Loss_G: 4.7893 Loss_D: 0.0820 D_real: 0.9691 D_fake: 0.0452
Epoch (136/200) Iteration (3651) Loss_G: 5.8384 Loss_D: 0.0694 D_real: 0.9531 D_fake: 0.0151
Epoch (138/200) Iteration (3701) Loss_G: 6.0576 Loss_D: 0.0264 D_real: 0.9799 D_fake: 0.0056
Epoch (139/200) Iteration (3751) Loss_G: 4.0465 Loss_D: 0.4976 D_real: 0.7709 D_fake: 0.0457
Epoch (141/200) Iteration (3801) Loss_G: 4.7491 Loss_D: 0.1910 D_real: 0.8837 D_fake: 0.0315
Epoch (143/200) Iteration (3851) Loss_G: 4.2405 Loss_D: 0.1179 D_real: 0.9232 D_fake: 0.0305
Epoch (145/200) Iteration (3901) Loss_G: 5.6623 Loss_D: 0.0517 D_real: 0.9650 D_fake: 0.0143
Epoch (147/200) Iteration (3951) Loss_G: 6.0612 Loss_D: 0.0621 D_real: 0.9945 D_fake: 0.0518
Epoch (149/200) Iteration (4001) Loss_G: 5.6867 Loss_D: 0.0420 D_real: 0.9844 D_fake: 0.0242
Epoch (151/200) Iteration (4051) Loss_G: 5.1841 Loss_D: 0.0464 D_real: 0.9794 D_fake: 0.0239
Epoch (152/200) Iteration (4101) Loss_G: 6.2106 Loss_D: 0.0395 D_real: 0.9781 D_fake: 0.0156
Epoch (154/200) Iteration (4151) Loss_G: 4.9452 Loss_D: 0.6044 D_real: 0.8094 D_fake: 0.1261
Epoch (156/200) Iteration (4201) Loss_G: 4.8802 Loss_D: 0.1568 D_real: 0.9167 D_fake: 0.0519
Epoch (158/200) Iteration (4251) Loss_G: 5.0978 Loss_D: 0.1355 D_real: 0.9360 D_fake: 0.0516
Epoch (160/200) Iteration (4301) Loss_G: 5.0344 Loss_D: 0.0716 D_real: 0.9492 D_fake: 0.0160
Epoch (162/200) Iteration (4351) Loss_G: 4.7368 Loss_D: 0.0711 D_real: 0.9471 D_fake: 0.0141
Epoch (163/200) Iteration (4401) Loss_G: 4.8459 Loss_D: 0.0736 D_real: 0.9525 D_fake: 0.0231
Epoch (165/200) Iteration (4451) Loss_G: 6.2494 Loss_D: 0.0727 D_real: 0.9949 D_fake: 0.0611
Epoch (167/200) Iteration (4501) Loss_G: 5.6498 Loss_D: 0.0530 D_real: 0.9784 D_fake: 0.0295
Epoch (169/200) Iteration (4551) Loss_G: 4.8751 Loss_D: 0.0585 D_real: 0.9637 D_fake: 0.0193
Epoch (171/200) Iteration (4601) Loss_G: 18.5738 Loss_D: 1.2638 D_real: 0.9987 D_fake: 0.4833
Epoch (173/200) Iteration (4651) Loss_G: 6.2833 Loss_D: 0.8649 D_real: 0.8324 D_fake: 0.2366
Epoch (175/200) Iteration (4701) Loss_G: 6.4607 Loss_D: 0.1329 D_real: 0.9816 D_fake: 0.0955
Epoch (176/200) Iteration (4751) Loss_G: 5.5655 Loss_D: 0.0907 D_real: 0.9637 D_fake: 0.0461
Epoch (178/200) Iteration (4801) Loss_G: 4.0551 Loss_D: 0.1175 D_real: 0.9240 D_fake: 0.0308
Epoch (180/200) Iteration (4851) Loss_G: 5.0634 Loss_D: 0.0568 D_real: 0.9633 D_fake: 0.0183
Epoch (182/200) Iteration (4901) Loss_G: 5.1921 Loss_D: 0.0655 D_real: 0.9688 D_fake: 0.0313
Epoch (184/200) Iteration (4951) Loss_G: 8.4480 Loss_D: 0.2072 D_real: 0.9966 D_fake: 0.1614
Epoch (186/200) Iteration (5001) Loss_G: 5.2179 Loss_D: 0.0526 D_real: 0.9717 D_fake: 0.0223
Epoch (188/200) Iteration (5051) Loss_G: 5.6508 Loss_D: 0.0322 D_real: 0.9892 D_fake: 0.0201
Epoch (189/200) Iteration (5101) Loss_G: 6.9098 Loss_D: 0.0177 D_real: 0.9938 D_fake: 0.0112
Epoch (191/200) Iteration (5151) Loss_G: 6.3866 Loss_D: 0.0124 D_real: 0.9949 D_fake: 0.0071
Epoch (193/200) Iteration (5201) Loss_G: 7.2608 Loss_D: 0.0313 D_real: 0.9754 D_fake: 0.0050
Epoch (195/200) Iteration (5251) Loss_G: 7.7534 Loss_D: 0.0154 D_real: 0.9946 D_fake: 0.0097
Epoch (197/200) Iteration (5301) Loss_G: 7.0825 Loss_D: 0.0106 D_real: 0.9950 D_fake: 0.0054
Epoch (199/200) Iteration (5351) Loss_G: 7.4502 Loss_D: 0.0076 D_real: 0.9979 D_fake: 0.0053
Finished training!
CPU times: total: 9min 33s
Wall time: 10min 34s
Begin training...
Epoch (1/200) Iteration (1) Loss_G: 1.7893 Loss_D: 3.2550 D_real: 0.2664 D_fake: 0.3662
Epoch (2/200) Iteration (51) Loss_G: 3.4757 Loss_D: 0.8228 D_real: 0.8536 D_fake: 0.2715
Epoch (3/200) Iteration (101) Loss_G: 4.5845 Loss_D: 0.5271 D_real: 0.8543 D_fake: 0.1388
Epoch (5/200) Iteration (151) Loss_G: 5.2458 Loss_D: 0.2388 D_real: 0.9584 D_fake: 0.1332
...
...
Epoch (199/200) Iteration (5351) Loss_G: 7.4502 Loss_D: 0.0076 D_real: 0.9979 D_fake: 0.0053
Finished training!
CPU times: total: 9min 33s
Wall time: 10min 34s
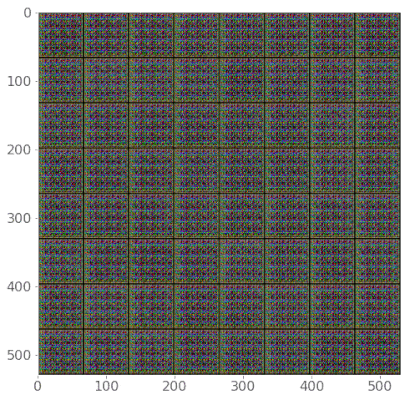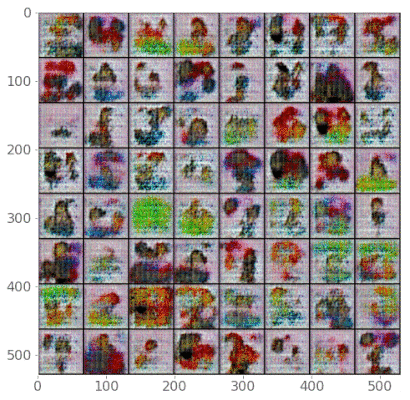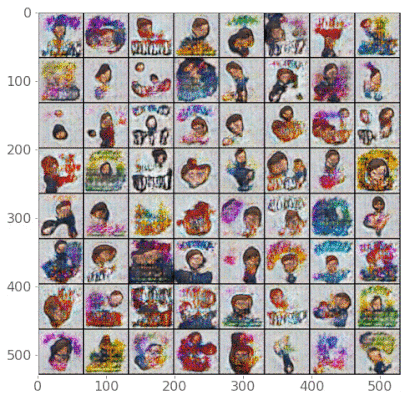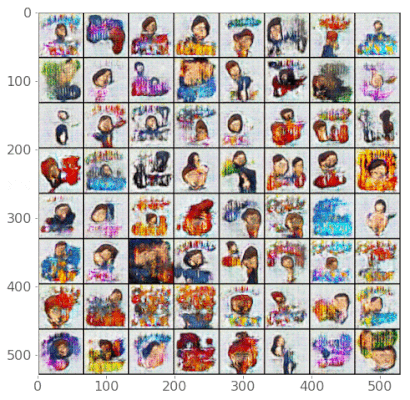
Now, here’s a fancy animation that shows how our generator got better over time
I could have trained for longer, but the results are pretty cool!
%%capture
fig = plt.figure(figsize=(6,6))
ims = [[plt.imshow(np.transpose(i,(1,2,0)), animated=True)] for i in img_list]
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)
# ani.save('bitmoji.gif', writer='imagemagick', fps=2)
# HTML(ani.to_jshtml()) # run this in a new cell to produce the below animation
Amintoosi [Ami22] utilized style transfer techniques for data augmentation in fire detection. To fully understand this paper, it is important to be familiar with Generative Adversarial Networks (GANs), Conditional GANs, Cycle GANs, image-to-image translation, Neural Style Transfer (NST), and StyleGANs.
Excersice:
Further Reading
NST papers:
Section 12.4 of Deep Learning with Python: Variational Autoencoders
Colab Variational autoencoders
Section 12.4 of Deep Learning with Python: Generative adversarial networks
GFPGAN aims at developing a Practical Algorithm for Real-world Face Restoration
Colab GFPGAN_inference
StyleGAN: A Style-Based Generator Architecture for Generative Adversarial Networks Wiki
3. Multi-input Networks#
Sometimes you’ll want to combine different types of data in a single network
The most common case is combining tabular data with image data, for example, using both real estate data and images of a house to predict its sale price:
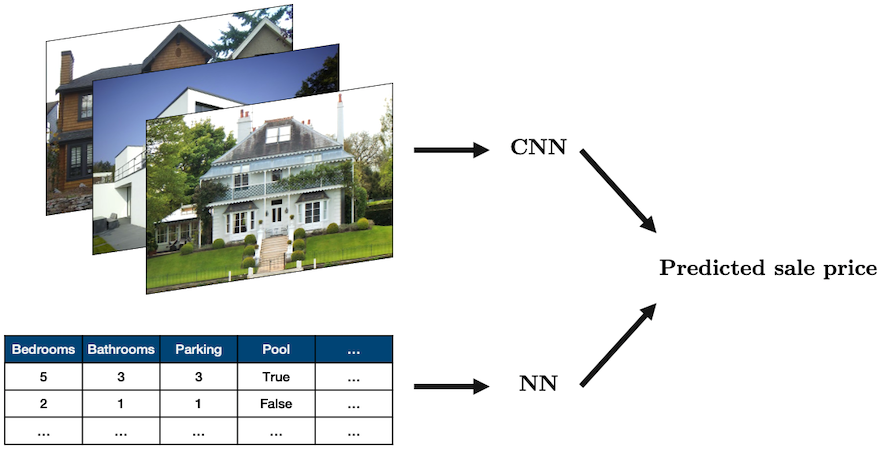
Source: “House” by oatsy40, “House in Vancouver” by pnwra, “House” by noona11 all licensed under CC BY 2.0.
In such a problem you may want to combine:
a NN for the tabular data
a CNN for the image data
The way we often do this is create these two models, and then combine them together into a model that produces a single output
This sounds complicated but it’s pretty easy! We only need one new ingredient which is a concatenation function:
torch.cat()Below is a simple example:
class MultiModel(nn.Module):
def __init__(self):
super().__init__()
self.cnn = nn.Sequential(
nn.Conv2d(3, 16, 3, 2, 1),
nn.ReLU(),
nn.Conv2d(16, 8, 5, 2, 1),
nn.ReLU(),
nn.Flatten(),
nn.Linear(1800, 5)
)
self.fc = nn.Sequential(
nn.Linear(10, 50),
nn.ReLU(),
nn.Linear(50, 5)
)
self.multi = nn.Sequential(
nn.Linear(10, 5),
nn.ReLU(),
nn.Linear(5, 1)
)
def forward(self, image, data):
x_cnn = self.cnn(image)
x_fc = self.fc(data)
x_multi = torch.cat((x_cnn, x_fc), dim=1)
return self.multi(x_multi)
model = MultiModel()
image = torch.randn(1, 3, 64, 64)
data = torch.randn(1, 10)
model(image, data).item()
-0.40757834911346436
The above network doesn’t really do anything but show that we can easily combine a CNN and fully connected NN!
4. Things I Haven’t Talked About#
Recurrent neural networks (coming in DSCI 575 and DSCI 574, good for sequential data like text and time series)
Bayesian neural networks (in one sentence: capture uncertainty by learning a distribution over the network parameters rather than learning point estimates)
Training at scale/distributed computing (coming in DSCI 525)
Working with other forms of data like time series (DSCI 574), text (DSCI 575), audio, video, etc.
Pruning (removing unnecessary weights from a deep network) and quantization (use a small data type for model weights and operations, e.g., integers rather than floats) to reduce memory foot print and increase speed
High-level PyTorch APIs: Ignite, Skorch, Pytorch-Lightning, etc.
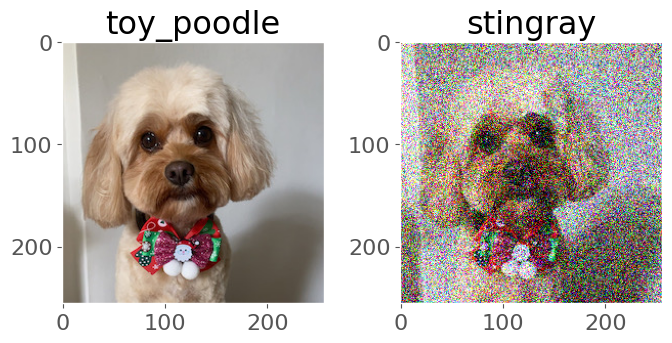
Adversarial examples. In one sentence: this is about “tricking” a model by adding some artifact, like noise, to the input image. See this OpenAI blog post or some work on adversarial stickers (more comining in DSCI 541)
densenet = models.densenet121(pretrained=True)
densenet.eval()
classes = json.load(open("data/imagenet_class_index.json"))
idx2label = [classes[str(k)][1] for k in range(len(classes))]
torch.manual_seed(0)
image = Image.open('img/evie.png')
image = transforms.functional.to_tensor(image).unsqueeze(0)
image_noise = image + 0.30 * torch.randn_like(image)
_, image_idx = torch.softmax(densenet(image), dim=1).topk(1)
_, image_noise_idx = torch.softmax(densenet(image_noise), dim=1).topk(1)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(7, 4))
ax1.imshow(np.transpose(image.squeeze(), (1, 2, 0)))
ax1.set_title(f"{idx2label[image_idx.item()]}")
ax2.imshow(np.transpose(image_noise.squeeze(), (1, 2, 0)))
ax2.set_title(f"{idx2label[image_noise_idx.item()]}")
plt.tight_layout()
Clipping input data to the valid range for imshow with RGB data ([0..1] for floats or [0..255] for integers).
Weight initiailization in layers:
We explored how the starting point of your optimization can affect the final result
The general rule for setting the weights in a neural network is to set them to be close to zero without being too small
PyTorch does this for you automatically, but if you want to make your code exactly reproducible and be in control of the initialization, you can do that too
It’s easy to do in PyTorch using the
.apply()method:
def weights_init(m):
if isinstance(m, nn.Conv2d):
torch.nn.init.xavier_uniform_(m.weight)
torch.nn.init.zeros_(m.bias)
model.apply(weights_init)
class example(torch.nn.Module):
def __init__(self):
super().__init__()
self.main = nn.Sequential(
nn.Conv2d(1, 3, (3, 3)),
nn.Flatten(),
nn.Linear(2028, 1000),
nn.ReLU(),
nn.Linear(1000, 10)
)
def forward(self, x):
out = self.main(x)
return out
def weights_init(m):
if isinstance(m, nn.Conv2d):
print("Initializing weights of a Conv2d layer!")
nn.init.normal_(m.weight, mean=0, std=0.1)
nn.init.zeros_(m.bias)
if isinstance(m, nn.Linear):
print("Initializing weights of a Linear layer!")
nn.init.xavier_uniform_(m.weight)
nn.init.zeros_(m.bias)
torch.manual_seed(123)
model = example()
model.apply(weights_init);
Initializing weights of a Conv2d layer!
Initializing weights of a Linear layer!
Initializing weights of a Linear layer!
5. Tom’s Cheat Sheet#
TABULAR DATA
Classification:
Logisitic Regression + feature engineer
XGBoost / LGBM + feature engineer
Neural network + feature engineer
Regression:
Linear Regression + feature engineer
XGBoost / LGBM + feature engineer
Neural network + feature engineer
IMAGE DATA
Use a CNN:
Option 1: if data is relatively simple, develop CNN from scratch:
Start with 3x3 filters with strides of 1 or 2
Number of filters proprtional to data complexity, usually 4, 8, 16, 24
The first convolutional layer should have more channels that the input data
Option 2: transfer learning
TIME SERIES DATA
AutoRegressive Integrated Moving Average (ARIMA) - more in 574
XGBoost / LGBM + feature engineer
Recurrent neural network (RNN) - more in 575/574
AUDIO, VIDEO, OTHER
Probably some kind of NN
References#
Mahmood Amintoosi. Style transfer for data augmentation in convolutional neural networks applied to fire detection. Computational Intelligence in Electrical Engineering, 13(4):97–114, 2022. URL: https://isee.ui.ac.ir/article_26042.html, doi:10.22108/isee.2021.124044.1490.
M.J. Zaki, W. Meira, and W. Meira. Data Mining and Machine Learning: Fundamental Concepts and Algorithms. Cambridge University Press, 2020. ISBN 9781108473989. URL: https://dataminingbook.info/.
6. The Lecture in Three Conjectures#
There is a world of deep learning out there. You now have the foundational skills to explore that world!
I personally feel that PyTorch is an amazing tool for deep learning and I hope that you’ll continue to use it in your future data science careers.
There is no magic bullet for solving data science problems. But, you don’t need to do things from scratch! Do your research, look at how others have approached a similar problem to yours, and leverage the work that’s already out there.


