
Regression#
Mahmood Amintoosi, Spring 2024
Computer Science Dept, Ferdowsi University of Mashhad
Show code cell content
# Auto-setup when running on Google Colab
import os
if 'google.colab' in str(get_ipython()) and not os.path.exists('/content/neural-networks'):
!git clone -q https://github.com/fum-cs/neural-networks.git /content/neural-networks
!pip --quiet install -r /content/neural-networks/requirements_colab.txt
%cd neural-networks/notebooks
Show code cell content
import warnings
warnings.filterwarnings("ignore")
import numpy as np
from sklearn.model_selection import train_test_split
# This is needed to render the plots
from utils.utils import *
Linear Model#
Suppose that the true model is denoted by \(y = b + m x + \epsilon\) and the estimated model denoted by \(\hat{y}\) (Eq. 23.2 of Zaki book [ZMM20]):
If we have:
then \(\hat{y}\) can be considered as dot product of two vectors:
If \(i^{th}\) instance is shown by \(\mathbf{x}_i\)
then:
Sum of Squared Error (SSE):
where:
Data Generation#
Synthetic Data Generation#
true_w0 = 1 # b in mx+b
true_w1 = 2 # m in mx+b
N = 100
# Data Generation
np.random.seed(42)
x = np.random.rand(N, 1)
epsilon = 0.1 * np.random.randn(N, 1)
y = true_w0 + true_w1 * x + epsilon
# Add a column of 1s to x
# ones = np.ones((N, 1))
# X = np.concatenate([ones, x],axis=1)
X = np.insert(x, 0, 1, axis=1)
print(x.shape, X.shape)
print(x[:3])
print(y[:3])
(100, 1) (100, 2)
[[0.37454012]
[0.95071431]
[0.73199394]]
[[1.75778494]
[2.87152788]
[2.47316396]]
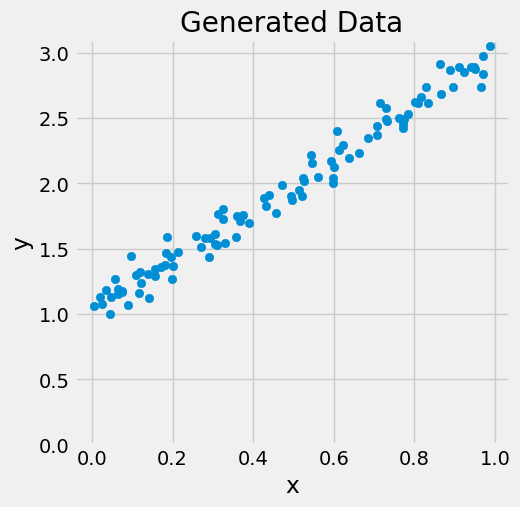
figure0(x, y)
Normal Equations#
The Normal Equations provide a closed-form solution for finding the optimal parameters (coefficients) that minimize the cost function (usually the mean squared error) in linear regression.
The Normal Equations are derived by setting the partial derivatives of the cost function with respect to each coefficient to zero.
The Closed Form Solution refers to finding the optimal parameters directly using a mathematical formula, rather than an iterative optimization process.
We have to minimize: \(||X\mathbf{w} - \mathbf{y}||_2^2\) wrt \(\mathbf{w}\), which is equal to the famous form \(min_{x}||Ax - b||_2^2\). Temporary we use \(\beta\), instead of \(\mathbf{w}\) and ignore the bold faces of letters; hence we have to minimize \(||X\beta-y||_2^2\)
We Know that (See Matrix Calculus in Appendix A and Wikipedia):
and if \(M\) be a symmetric matrix:
Hence:
Set the derivative equal to zero:
and with our previous notation: \(\mathbf{w} = (X^TX)^{-1}X^T\mathbf{y}\)
w = np.linalg.inv(X.T @ X) @ X.T @ y
w
array([[1.02150962],
[1.95402268]])
Using Scikit-learn#
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(x, y)
print(linreg.intercept_, linreg.coef_)
[1.02150962] [[1.95402268]]
If we have augmented data matrix \(X \in \mathbb{R}^{n\times (d+1)}\), we have to set fit_intercept=False. In eq. (23.20) of Zaki this is denoted by \(\tilde{D}\).
linreg = LinearRegression(fit_intercept=False)
linreg.fit(X, y)
print(linreg.coef_)
[[1.02150962 1.95402268]]
Bivariate Regression#
In bivariate regression, we have two variables: one is the predictor variable (also known as the feature), and the other is the response variable (also known as the target).
Predictor Variable (Feature):
The predictor variable (often denoted as x) is the input variable that we use to predict or explain the variation in the response variable.
In machine learning, this is equivalent to a feature. Features represent the characteristics or attributes of the data points.
For example, in a housing price prediction model, features could include square footage, number of bedrooms, location, etc.
Response Variable (Target):
The response variable (often denoted as y) is the output variable that we are trying to predict or understand based on the predictor variable.
In machine learning, this is equivalent to the target. The target represents the value we want to predict.
For the housing price prediction model, the target would be the actual sale price of a house.
So, in summary, bivariate regression involves analyzing the relationship between two variables: one (the feature) is used to predict or explain the behavior of the other (the target). These terms are commonly used in both statistics and machine learning.
For further information about Multivariate Multiple Regression, see this blog post of Faradars.
According to Sections 23.2 of Zaki book, \(b\) and \(w\) in \(\hat{y}=b+wx\), can be calculated as follows:
\(b = \mu_y - w\mu_x, \quad w = \frac{cov(x,y)}{var(x)}\)
x.squeeze().shape, y.shape
((100,), (100, 1))
# Setting ddof=0 to use the biased estimator
covariance_matrix = np.cov(x.squeeze(), y.squeeze(), ddof=0)
w = covariance_matrix[0, 1] / np.var(x)
b = np.mean(y) - w * np.mean(x)
b, w
(1.0215096157546752, 1.954022677287696)
sigma_xy = np.mean((y - np.mean(y)) * (x - np.mean(x)))
w = sigma_xy / np.var(x)
b = np.mean(y) - w * np.mean(x)
b, w
# sigma_xy, sigma_xy/np.var(x), w
(1.0215096157546752, 1.954022677287696)
Gradient Descent#
In this section we are going to introduce the basic concepts underlying gradient descent. Some materials are borrowed from D2L.
One-Dimensional Gradient Descent#
Gradient descent in one dimension is an excellent example to explain why the gradient descent algorithm may reduce the value of the objective function. Consider some continuously differentiable real-valued function \(f: \mathbb{R} \rightarrow \mathbb{R}\). Using a Taylor expansion we obtain
That is, in first-order approximation \(f(x+h)\) is given by the function value \(f(x)\) and the first derivative \(f'(x)\) at \(x\). It is not unreasonable to assume that for small \(h\) moving in the direction of the negative gradient will decrease \(f\). To keep things simple we pick a fixed step size \(\eta > 0\) and choose \(h = -\eta f'(x)\). Plugging this into the Taylor expansion above we get
If the derivative \(f'(x) \neq 0\) does not vanish we make progress since \(\eta f'^2(x)>0\). Moreover, we can always choose \(\eta\) small enough for the higher-order terms to become irrelevant. Hence we arrive at
This means that, if we use
to iterate \(x\), the value of function \(f(x)\) might decline. Therefore, in gradient descent we first choose an initial value \(x\) and a constant \(\eta > 0\) and then use them to continuously iterate \(x\) until the stop condition is reached, for example, when the magnitude of the gradient \(|f'(x)|\) is small enough or the number of iterations has reached a certain value.
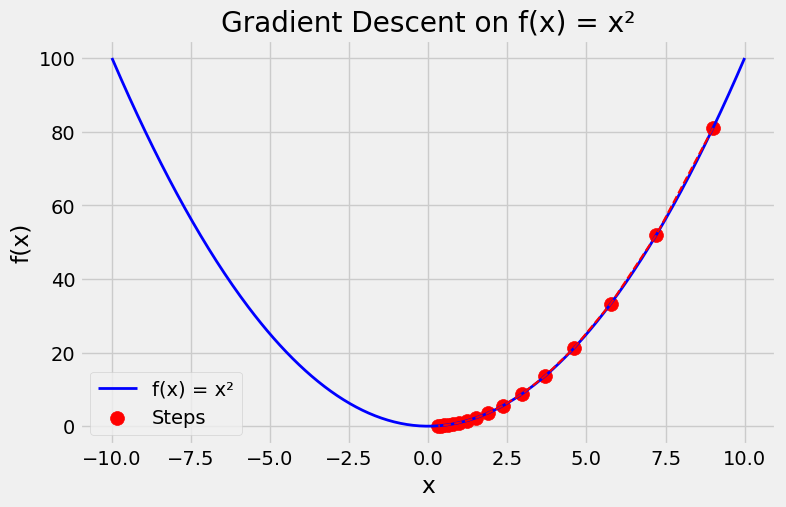
Gradient Descent on \(f(x)=x^2\)#
For simplicity we choose the objective function \(f(x)=x^2\) to illustrate how to implement gradient descent. Although we know that \(x=0\) is the solution to minimize \(f(x)\), we still use this simple function to observe how \(x\) changes.
# Defining a simple quadratic function and its derivative
f = lambda x: x**2
f_prime = lambda x: 2 * x
# Generating values
x = np.linspace(-10, 10, 400)
y = f(x)
# Gradient descent settings
learning_rate = 0.1
x_start = 9.0 # Starting point
steps = [x_start]
n_iterations = 15
# Gradient Descent Iteration
for _ in range(n_iterations):
print(
"x = {:4.2f}, f'(x) = {:5.2f}, -lr*f'(x)={:5.2f}".format(
x_start, f_prime(x_start), -learning_rate * f_prime(x_start)
)
)
x_start = x_start - learning_rate * f_prime(x_start)
steps.append(x_start)
# Plotting the function
plt.figure(figsize=(8, 5))
plt.plot(x, y, lw=2, color="blue", label="f(x) = x²")
# Plotting the steps
plt.scatter(steps, f(np.array(steps)), color="red", s=100, label="Steps")
plt.plot(steps, f(np.array(steps)), color="red", linestyle="--", lw=1.5)
# Annotations and labels
plt.title("Gradient Descent on f(x) = x²")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()
x = 9.00, f'(x) = 18.00, -lr*f'(x)=-1.80
x = 7.20, f'(x) = 14.40, -lr*f'(x)=-1.44
x = 5.76, f'(x) = 11.52, -lr*f'(x)=-1.15
x = 4.61, f'(x) = 9.22, -lr*f'(x)=-0.92
x = 3.69, f'(x) = 7.37, -lr*f'(x)=-0.74
x = 2.95, f'(x) = 5.90, -lr*f'(x)=-0.59
x = 2.36, f'(x) = 4.72, -lr*f'(x)=-0.47
x = 1.89, f'(x) = 3.77, -lr*f'(x)=-0.38
x = 1.51, f'(x) = 3.02, -lr*f'(x)=-0.30
x = 1.21, f'(x) = 2.42, -lr*f'(x)=-0.24
x = 0.97, f'(x) = 1.93, -lr*f'(x)=-0.19
x = 0.77, f'(x) = 1.55, -lr*f'(x)=-0.15
x = 0.62, f'(x) = 1.24, -lr*f'(x)=-0.12
x = 0.49, f'(x) = 0.99, -lr*f'(x)=-0.10
x = 0.40, f'(x) = 0.79, -lr*f'(x)=-0.08
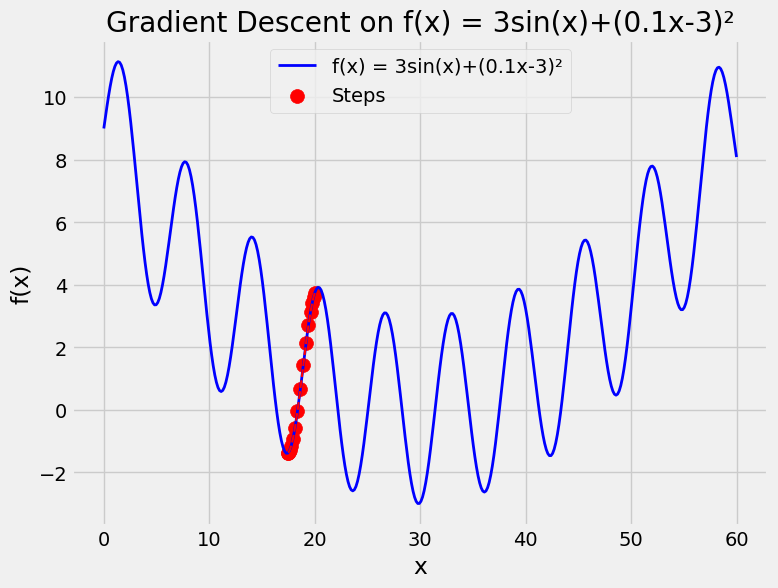
And another function see \(f(x)=3\sin(x)+(0.1x-3)^2\) where you solved that in ADS course using PSO.
# Defining a simple quadratic function and its derivative
f = lambda x: 3 * np.sin(x) + (0.1 * x - 3) ** 2
f_prime = lambda x: 3 * np.cos(x) + 0.2 * (0.1 * x - 3)
# Generating values
x = np.linspace(0, 60, 400)
y = f(x)
# Gradient descent settings
learning_rate = 0.1
x_start = 20 # Starting point
steps = [x_start]
n_iterations = 15
# Gradient Descent Iteration
for _ in range(n_iterations):
x_start = x_start - learning_rate * f_prime(x_start)
steps.append(x_start)
# Plotting the function
plt.figure(figsize=(8, 6))
plt.plot(x, y, lw=2, color="blue", label="f(x) = 3sin(x)+(0.1x-3)²")
# Plotting the steps
plt.scatter(steps, f(np.array(steps)), color="red", s=100, label="Steps")
plt.plot(steps, f(np.array(steps)), color="red", linestyle="--", lw=1.5)
# Annotations and labels
plt.title("Gradient Descent on f(x) = 3sin(x)+(0.1x-3)²")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.legend()
plt.grid(True)
plt.show()
Using Gradient Descent for Regression in Machine Learning#
Here we use training data for estimation of the model parameters and report the error on test data
# Reproduce our data
true_w0 = 1 # b in mx+b
true_w1 = 2 # m in mx+b
N = 100
# Data Generation
np.random.seed(42)
x = np.random.rand(N, 1)
epsilon = 0.1 * np.random.randn(N, 1)
y = true_w0 + true_w1 * x + epsilon
X = np.insert(x, 0, 1, axis=1)
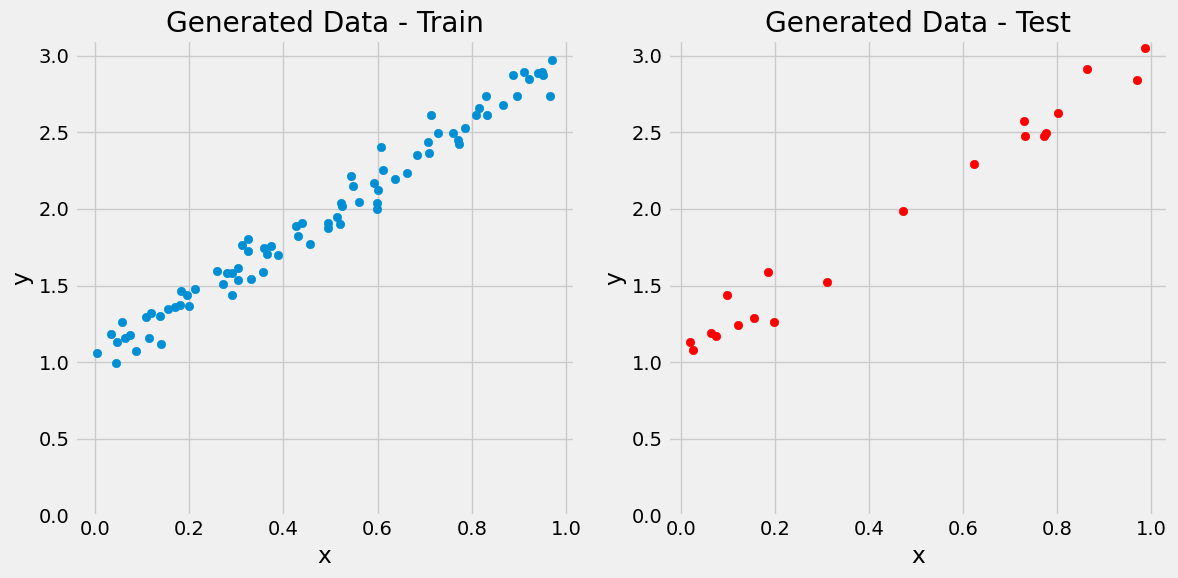
Train-Test Split#
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
x_train.shape, y_train.shape
((80, 2), (80, 1))
figure1(x_train, y_train, x_test, y_test)
(<Figure size 1200x600 with 2 Axes>,
array([<Axes: title={'center': 'Generated Data - Train'}, xlabel='x', ylabel='y'>,
<Axes: title={'center': 'Generated Data - Test'}, xlabel='x', ylabel='y'>],
dtype=object))
Step 0: Random Initialization#
# Step 0 - Initializes parameters "b" and "w" randomly
np.random.seed(42)
w = np.random.randn(2, 1)
print(w)
[[ 0.49671415]
[-0.1382643 ]]
Step 1: Compute Model’s Predictions#
# Step 1 - Computes our model's predicted output - forward pass
# y_hat = b + m * x_train
y_hat = w[0] + w[1] * x_train[:, 1]
y_hat[:3]
array([0.39881299, 0.41404593, 0.36925186])
y_hat = x_train @ w
y_hat[:3]
array([[0.39881299],
[0.41404593],
[0.36925186]])
figure2(x_train, y_train, w[0], w[1])
(<Figure size 600x600 with 1 Axes>, <Axes: xlabel='x', ylabel='y'>)
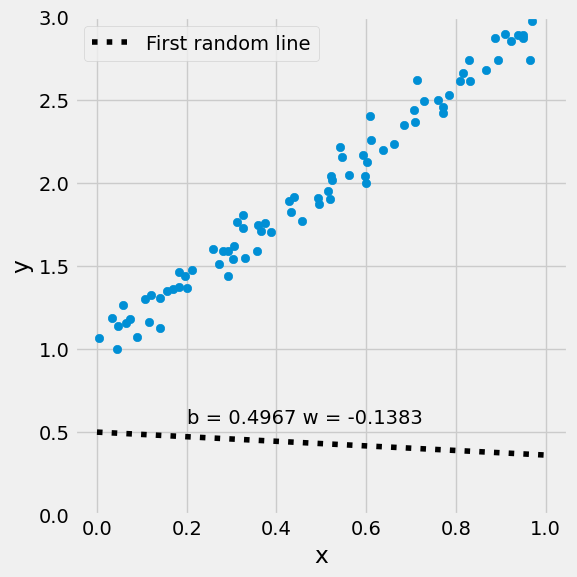
Step 2: Compute the Loss#
print(y_train[0], y_hat[0])
figure3(x_train, y_train, w[0], w[1])
[2.36596945] [0.39881299]
(<Figure size 600x600 with 1 Axes>, <Axes: xlabel='x', ylabel='y'>)
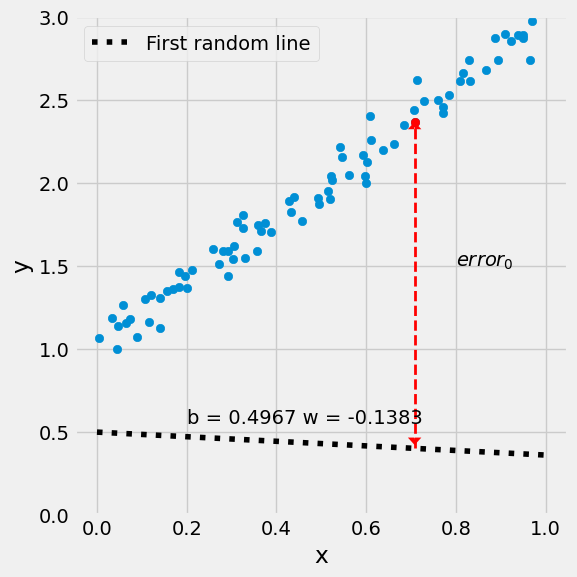
# Step 2 - Computing the loss
# We are using ALL data points, so this is BATCH gradient
# descent. How wrong is our model? That's the error!
error = y_hat - y_train
print(error.shape)
# It is a regression, so it computes mean squared error (MSE)
loss = (error**2).mean()
print(loss)
(80, 1)
2.6401126993616817
Loss Surface#
w0s, w1s, all_losses = mesh_losses(true_w0, true_w1, x_train, y_train)
figure4(x_train, y_train, w[0], w[1], w0s, w1s, all_losses)
(<Figure size 1200x600 with 2 Axes>,
(<Axes3D: title={'center': 'Loss Surface'}, xlabel='b', ylabel='w'>,
<Axes: title={'center': 'Loss Surface'}, xlabel='b', ylabel='w'>))
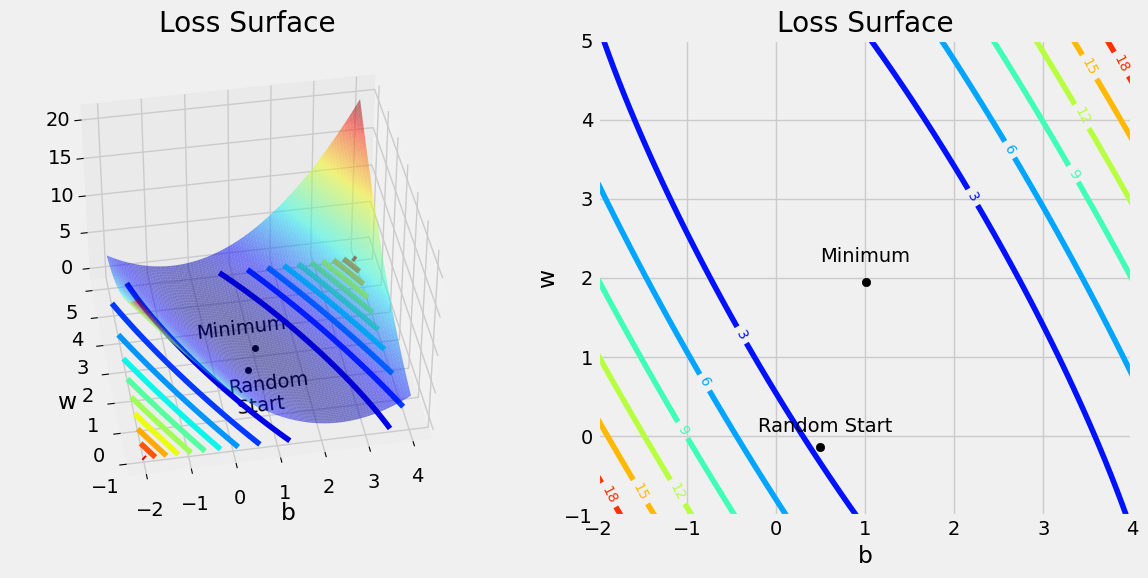
Step 3: Compute the Gradients#
# Step 3 - Computes gradients for both "b" and "w" parameters
w0_grad = 2 * error.mean()
# w1_grad = 2 * (x_train[:,1] * error).mean() # Wrong!
w1_grad = 2 * (np.delete(x_train, 0, axis=1) * error).mean()
print(w0_grad, w1_grad)
-3.0224384959608583 -1.7706733515907813
(x_train * error).shape
(80, 2)
Vectorized form
# w_grad = 2 * (x_train * error).mean() # Wrong
w_grad = 2 * (x_train * error).mean(axis=0)
print(w_grad.shape, w_grad)
w_grad = np.reshape(w_grad, (2, 1))
print(w_grad.shape, w_grad)
(2,) [-3.0224385 -1.77067335]
(2, 1) [[-3.0224385 ]
[-1.77067335]]
Backpropagation#
Step 4: Update the Parameters#
print(w.shape, w_grad.shape)
(2, 1) (2, 1)
# Sets learning rate - this is "eta" ~ the "n" like Greek letter
lr = 0.1
print(w[0], w[1])
# Step 4 - Updates parameters using gradients and the
# learning rate
# w[0] = w[0] - lr * w0_grad
# w[1] = w[1] - lr * w1_grad
w = w - lr * w_grad
print(w)
print(w[0])
[0.49671415] [-0.1382643]
[[0.798958 ]
[0.03880303]]
[0.798958]
figure9(x_train, y_train, w[0], w[1])
(<Figure size 600x600 with 1 Axes>, <Axes: xlabel='x', ylabel='y'>)
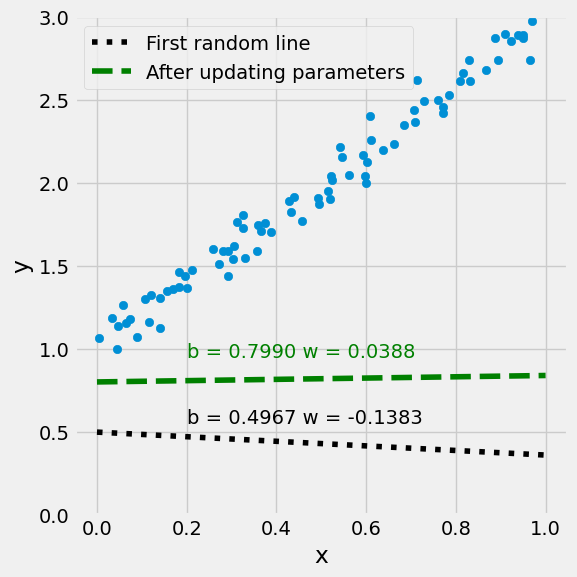
Step 5: Repeat the above updating!#
# Initializes parameters "b" and "w" randomly
np.random.seed(42)
w = np.random.randn(2, 1)
lr = 0.3
num_epochs = 50
Losses = np.empty(num_epochs)
for epoch in range(num_epochs):
y_hat = x_train @ w
error = y_hat - y_train
loss = (error**2).mean()
Losses[epoch] = loss
w_grad = 2 * (x_train * error).mean(axis=0)
w_grad = np.reshape(w_grad, (2, 1))
w = w - lr * w_grad
w
array([[1.11648206],
[1.75056848]])
figure9(x_train, y_train, w[0], w[1])
(<Figure size 600x600 with 1 Axes>, <Axes: xlabel='x', ylabel='y'>)
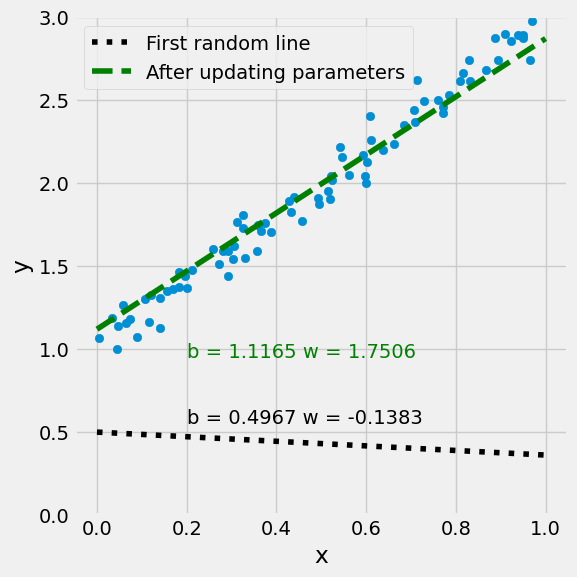
plt.plot(Losses)
[<matplotlib.lines.Line2D at 0x1a31f4dce50>]
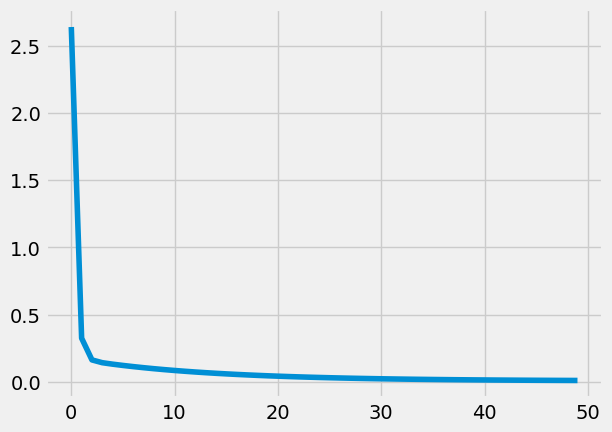
Using PyTorch auto grad#
PyTorch is a Python-based tool for scientific computing that provides several main features:
torch.Tensor, an n-dimensional array similar to that ofnumpy, but which can run on GPUsComputational graphs for building neural networks
Automatic differentiation for training neural networks (more on this next lecture)
You can install PyTorch from: https://pytorch.org/
import torch
from torch import autograd
# Initializes parameters "b" and "w" randomly
np.random.seed(42)
b = np.random.randn(1)
w = np.random.randn(1)
b = torch.tensor(b, requires_grad=True)
w = torch.tensor(w, requires_grad=True)
xTrain = torch.tensor(x_train) # xTrain is a pyTorch Tensor
yTrain = torch.tensor(y_train) # yTrain is a pyTorch Tensor
Backward#
Differntiationg using backward function
https://pytorch.org/tutorials/beginner/pytorch_with_examples.html
np.random.seed(42)
w = np.random.randn(2, 1)
w = torch.tensor(w, requires_grad=True)
xTrain = torch.tensor(x_train) # xTrain is a pyTorch Tensor
yTrain = torch.tensor(y_train) # yTrain is a pyTorch Tensor
lr = 0.3
num_epochs = 50
for epoch in range(num_epochs):
y_hat = xTrain @ w
error = y_hat - yTrain
loss = (error**2).mean(axis=0)
# محاسبه دستی مشتق را حذف کرده و به جاش مشتق خودکار را قرار می دهیم
loss.backward()
with torch.no_grad():
w -= lr * w.grad
# Manually zero the gradients after updating weights
w.grad = None
w
tensor([[1.1165],
[1.7506]], dtype=torch.float64, requires_grad=True)
https://pytorch.org/tutorials/beginner/pytorch_with_examples.html
PyTorch: Defining new autograd functions
PyTorch: nn module
PyTorch: optim
PyTorch: Custom nn Modules
Using PyTorch library#
import torch
import torch.nn as nn
# اگر از نوع دابل باشد خطا خواهیم گرفت
# x_train.dtype is float64
xTrain = torch.tensor(x_train, dtype=torch.float32)
yTrain = torch.tensor(y_train, dtype=torch.float32)
# همان مدل ساده قبلی با یک ورودی و یک خروجی، بایاس دارد
# در وضعیت جدید که یک ستون به دادهها اضافه کردهایم، یا باید فقط از ستون دوم استفاده کنیم
# یا مدل را بدون بایاس تعریف کنیم
model = nn.Linear(2, 1, bias=False)
learning_rate = 0.3
f = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
num_epochs = 50
for epoch in range(num_epochs):
y_hat = model(xTrain)
loss = f(y_hat, yTrain)
loss.backward() # backward propagation: calculate gradients
optimizer.step() # update the weights
optimizer.zero_grad() # clear out the gradients from the last step loss.backward()
print(model)
print(model.bias)
print(model.weight)
print(model.weight[0])
print(model.weight[0][0])
print(model.weight[0][0].item())
print(model.weight[0].detach().numpy()[0])
Linear(in_features=2, out_features=1, bias=False)
None
Parameter containing:
tensor([[1.0368, 1.9074]], requires_grad=True)
tensor([1.0368, 1.9074], grad_fn=<SelectBackward0>)
tensor(1.0368, grad_fn=<SelectBackward0>)
1.0367742776870728
1.0367743
w = model.weight[0].detach().numpy()
w = np.reshape(w, (2, 1))
figure9(x_train, y_train, w[0], w[1])
(<Figure size 600x600 with 1 Axes>, <Axes: xlabel='x', ylabel='y'>)
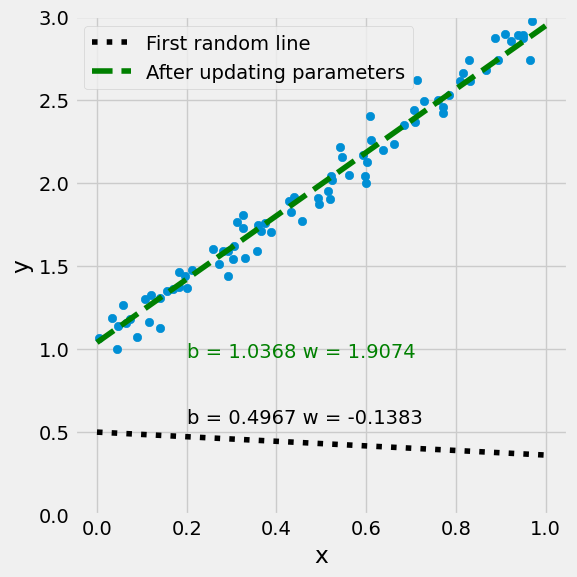
Further Reading:
Why use gradient descent for linear regression, when a closed-form math solution is available?
Some of the previous MSc thesis related to regression (In Persian):

