k-Nearest Neighbors and Classification Evaluation Metrics

k-Nearest Neighbors and Classification Evaluation Metrics#

This notebook covers:

Review of k-Nearest Neighbors (kNN) algorithm
Classification evaluation metrics: Accuracy, Precision, Recall, and F1-Score

Review of k-Nearest Neighbors (kNN)#

The k-Nearest Neighbors algorithm - which we saw in Hyperparameters and Model Validation - is a non-parametric, instance-based learning method used for classification and regression. The algorithm works by finding the k training samples closest in distance to a new sample and predicting the class label based on a majority vote.

Key Characteristics of kNN:#

Non-parametric: The algorithm doesn’t make assumptions about the underlying data distribution.
Instance-based (lazy learning): No explicit training phase; the model simply stores the training data.
Distance-based: Predictions are made based on the distance between points.

The kNN Algorithm (as described in Duda et al.):#

Store all training samples with their class labels.
For a new sample x:
- Calculate the distance between x and all training samples.
- Select the k closest training samples (k-nearest neighbors).
- Assign the class label based on majority voting among the k neighbors.

Distance Metrics:#

The most common distance metrics used in kNN are:

Euclidean Distance: \(d(x, y) = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}\)
Manhattan Distance: \(d(x, y) = \sum_{i=1}^{n} |x_i - y_i|\)
Minkowski Distance: \(d(x, y) = (\sum_{i=1}^{n} |x_i - y_i|^p)^{1/p}\)

Let’s implement and visualize the kNN algorithm:

# Generate a simple dataset
X, y = make_blobs(n_samples=300, centers=3, random_state=42, cluster_std=3)

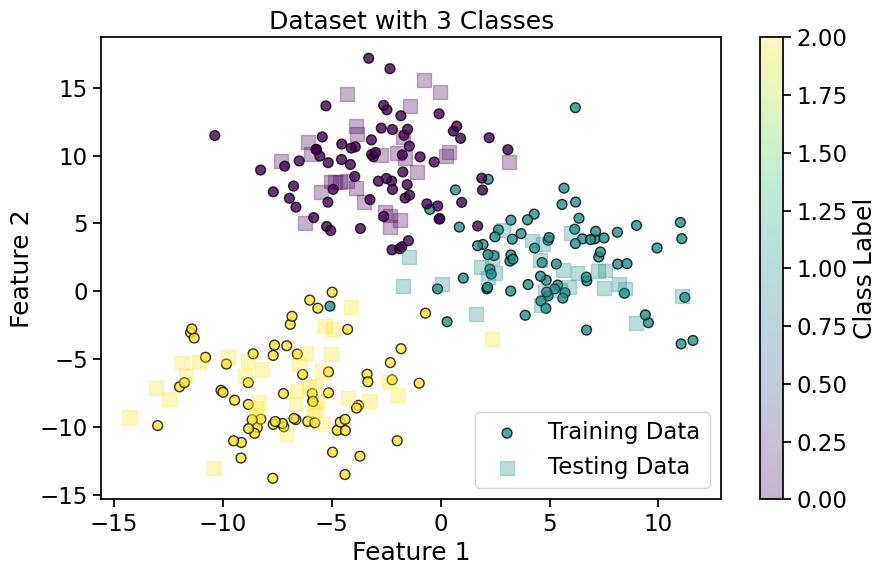
_images/7fc094e323759f77e52448584f8df2dd29073159aeb2976ac73ef12e54cb72c2.png

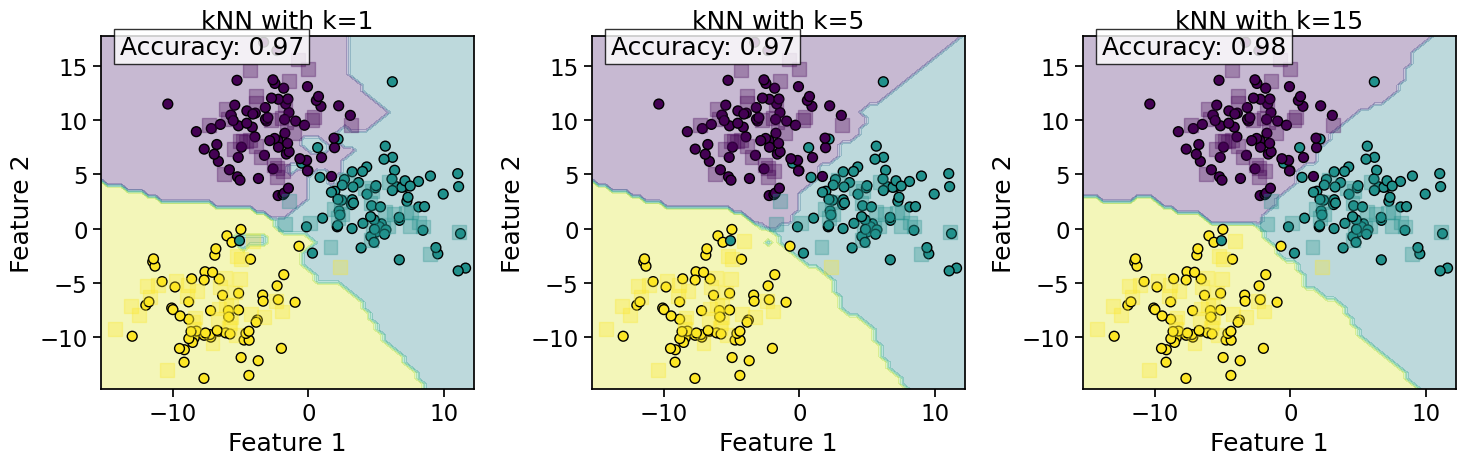
_images/0a5d4d5874b0996a04cf5ec42fe403d80e6ea90a16712e54499d61a3abddac96.png

Observations on kNN Behavior:#

Effect of k:
- Small k: Decision boundaries are more complex and can lead to overfitting
- Large k: Decision boundaries are smoother but may miss important patterns
Computational Complexity:
- Training: O(1) - just stores the data
- Prediction: O(nd) where n is the number of training samples and d is the number of features
Curse of Dimensionality:
- As the number of dimensions increases, the distance metric becomes less meaningful
- In high dimensions, all points tend to be equidistant from each other

Classification Evaluation Metrics#

To evaluate the performance of classification models, we need appropriate metrics. The choice of metric depends on the problem context and the relative importance of different types of errors.

Confusion Matrix#

A confusion matrix is a table that describes the performance of a classification model. For a binary classification problem, it contains:

True Positives (TP): Correctly predicted positive cases
False Positives (FP): Incorrectly predicted positive cases (Type I error)
True Negatives (TN): Correctly predicted negative cases
False Negatives (FN): Incorrectly predicted negative cases (Type II error)

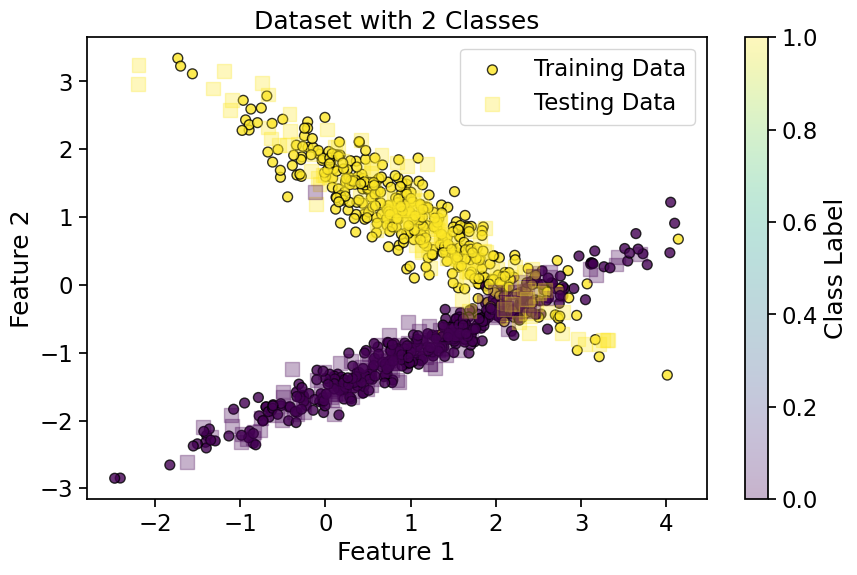
Let’s create a binary classification problem using make_classification and visualize its confusion matrix:

# Generate a binary classification dataset
X_binary, y_binary = make_classification(n_samples=1000, n_features=2, n_informative=2, 
                                         n_redundant=0, n_clusters_per_class=1, random_state=42)

_images/de1ebafab7bcf1f9b7e9b38e4f0faaae9f3945353cd7e882e5f4c7df20f2801b.png

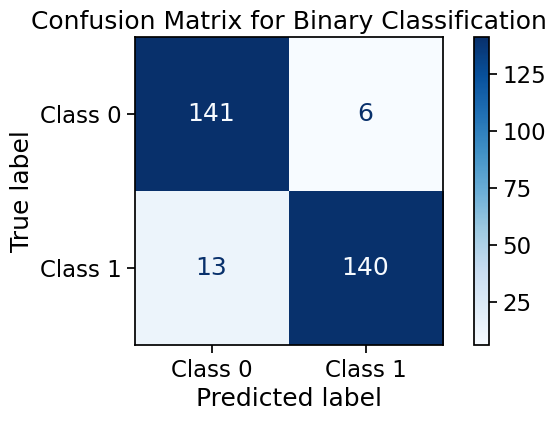
_images/b0df882f63f3c9584424ab0f19208d26bdf8cefb092d9ad3bf636466174504c4.png

True Negatives (TN): 141
False Positives (FP): 6
False Negatives (FN): 13
True Positives (TP): 140

Accuracy#

Accuracy is the ratio of correctly predicted instances to the total instances.

\[\text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN}\]

Pros:

Simple and intuitive
Works well for balanced datasets

Cons:

Misleading for imbalanced datasets
Doesn’t distinguish between types of errors

# Calculate accuracy
acc = accuracy_score(y_test_bin, y_pred_bin)
print(f"Accuracy: {acc:.4f}")

# Manual calculation
acc_manual = (tp + tn) / (tp + tn + fp + fn)
print(f"Manually calculated accuracy: {acc_manual:.4f}")

Accuracy: 0.9367
Manually calculated accuracy: 0.9367

Precision & Recall#

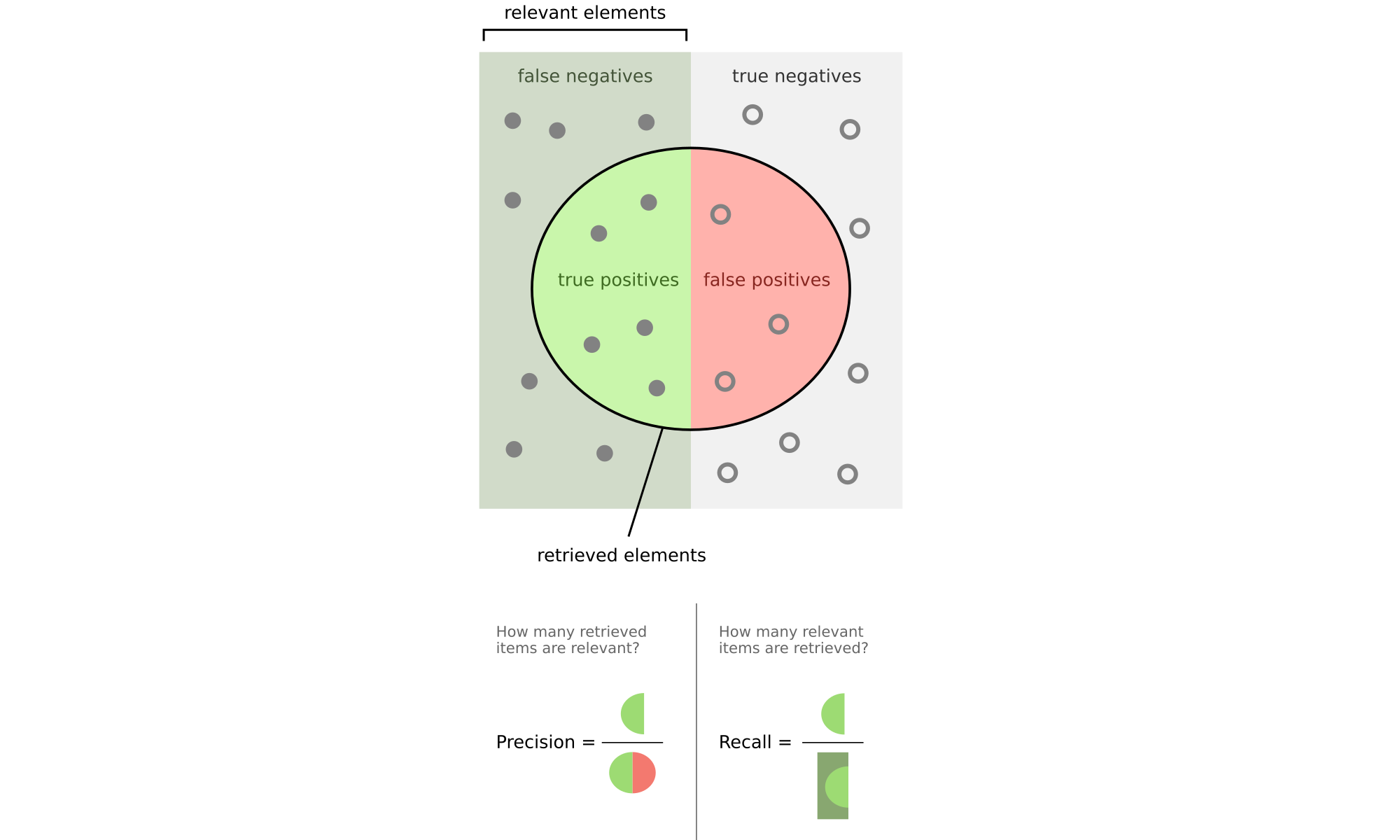
Precision#

Precision is the ratio of correctly predicted positive observations to the total predicted positives. It answers the question: “Of all instances predicted as positive, how many are actually positive?”

\[\text{Precision} = \frac{TP}{TP + FP}\]

Key Applications and Examples:

Spam Email Detection (تشخیص ایمیل اسپم) - incorrectly flagging important emails is costly
Medical Testing (آزمایش پزشکی) - avoiding false diagnoses that lead to unnecessary treatment
Autonomous Vehicles (خودروهای خودران) - misidentifying obstacles could cause dangerous reactions

Pros:

Critical when false positives (FP) have severe consequences
Essential for applications where incorrect positive predictions are costly
Particularly valuable in information retrieval systems where relevance is key

Cons:

Ignores false negatives (may miss important cases)
Can be misleadingly high if the model is overly conservative in predictions
Not sufficient alone for imbalanced datasets where negatives dominate

# Calculate precision
prec = precision_score(y_test_bin, y_pred_bin)
print(f"Precision: {prec:.4f}")

# Manual calculation
prec_manual = tp / (tp + fp) if (tp + fp) > 0 else 0
print(f"Manually calculated precision: {prec_manual:.4f}")

Precision: 0.9589
Manually calculated precision: 0.9589

Recall (Sensitivity)#

Recall is the ratio of correctly predicted positive observations to all actual positives. It answers the question: “Of all actual positive instances, how many did we predict correctly?”

\[\text{Recall} = \frac{TP}{TP + FN}\]

Key Applications and Examples:

Medical Diagnostics (تشخیص پزشکی)
Fraud Detection (تشخیص تقلب)
Landmine Detection (تشخیص مین‌های زمینی)
Security Surveillance (نظارت امنیتی)
Earthquake Early Warning Systems (سیستم‌های هشدار زودهنگام زلزله)
Cybersecurity Threat Detection (تشخیص تهدیدات سایبری)
Search and Rescue Operations (عملیات جستجو و نجات)

Pros:

Critical when the cost of false negatives (FN) is high (e.g., life-threatening scenarios).
Essential for medical screening and public safety applications.

Cons:

Does not account for false positives (FP) (may lead to unnecessary alerts).
Can be inflated artificially if a model labels everything as positive.

Trade-off Note: In many real-world systems, there’s an inverse relationship between precision and recall - improving one typically worsens the other. The right balance depends on which type of error (FP vs FN) is more costly for your specific application.

# Calculate recall
rec = recall_score(y_test_bin, y_pred_bin)
print(f"Recall: {rec:.4f}")

# Manual calculation
rec_manual = tp / (tp + fn) if (tp + fn) > 0 else 0
print(f"Manually calculated recall: {rec_manual:.4f}")

Recall: 0.9150
Manually calculated recall: 0.9150

2.5 F1-Score#

F1-Score is the harmonic mean of Precision and Recall. It provides a balance between precision and recall.

\[\text{F1-Score} = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}\]

Pros:

Balances precision and recall
Works well for imbalanced datasets

Cons:

May not be appropriate if one metric is more important than the other
Doesn’t consider true negatives

# Calculate F1-score
f1 = f1_score(y_test_bin, y_pred_bin)
print(f"F1-Score: {f1:.4f}")

# Manual calculation
f1_manual = 2 * (prec_manual * rec_manual) / (prec_manual + rec_manual) if (prec_manual + rec_manual) > 0 else 0
print(f"Manually calculated F1-Score: {f1_manual:.4f}")

F1-Score: 0.9365
Manually calculated F1-Score: 0.9365

Precision-Recall Trade-off#

There is often a trade-off between precision and recall. Increasing one typically decreases the other.

Let’s visualize this trade-off by adjusting the decision threshold for a probabilistic classifier:

# Generate a new dataset
X_new, y_new = make_classification(n_samples=1000, n_features=2, n_informative=2, 
                                   n_redundant=0, random_state=42, weights=[0.7, 0.3])

# Split the data
X_train_new, X_test_new, y_train_new, y_test_new = train_test_split(X_new, y_new, 
                                                                     test_size=0.3, random_state=42)

# Visualize the dataset
plt.figure(figsize=(10, 6))
plt.scatter(X_train_new[:, 0], X_train_new[:, 1], c=y_train_new, cmap='viridis', s=50, alpha=0.8, edgecolors='k')
plt.scatter(X_test_new[:, 0], X_test_new[:, 1], c=y_test_new, cmap='viridis', s=100, alpha=0.3, marker='s')
plt.title('Dataset with 2 Classes')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(['Training Data', 'Testing Data'])
plt.colorbar(label='Class Label')
plt.show()

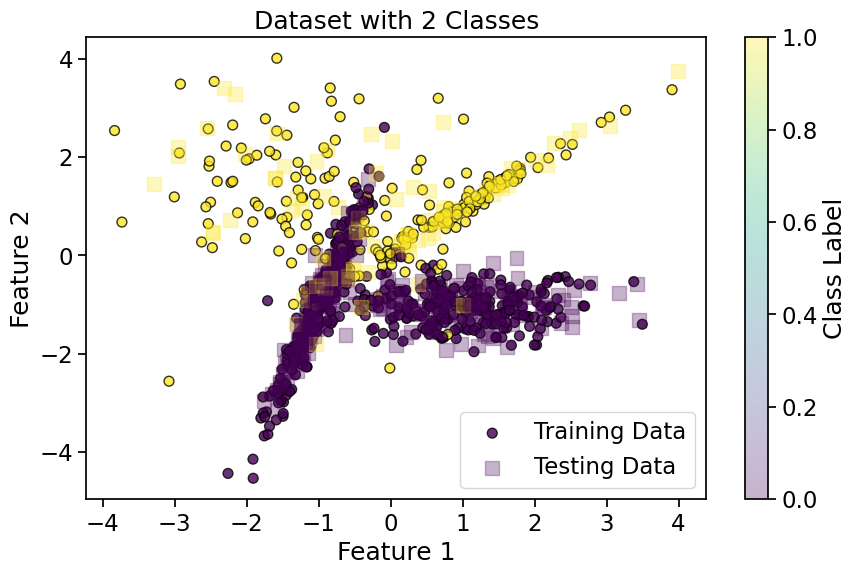
_images/a31dadce595178fe7af75ecd8735e04a3d03264a94b51ac30329478763f14fed.png

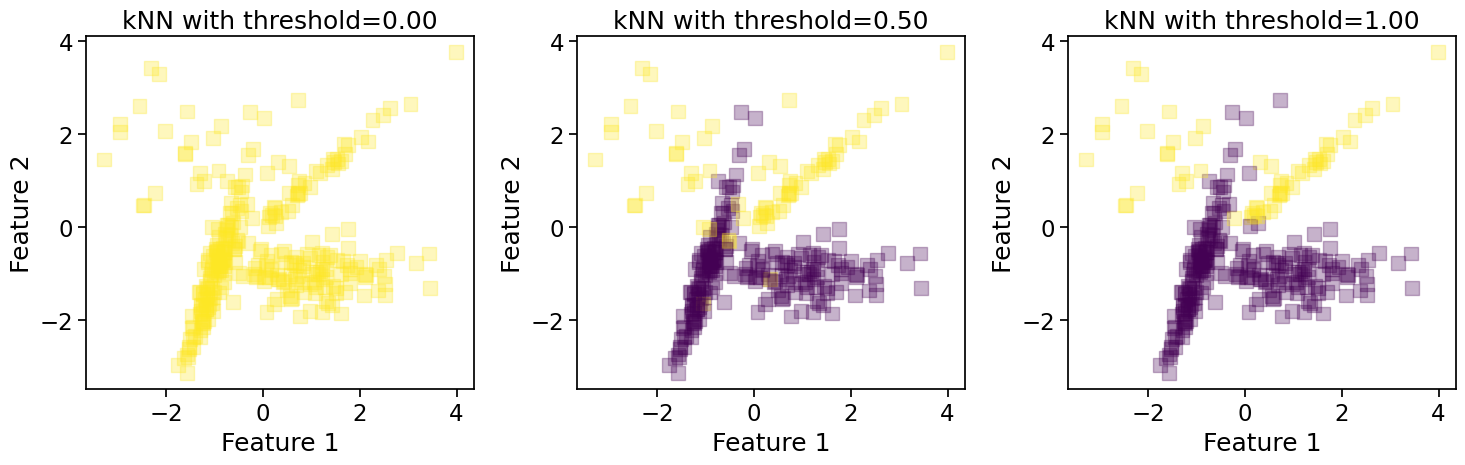
_images/2573e0929ca1f0f8051a42b11f1cfc15a7d0af1a623b17540055e2af2f794341.png

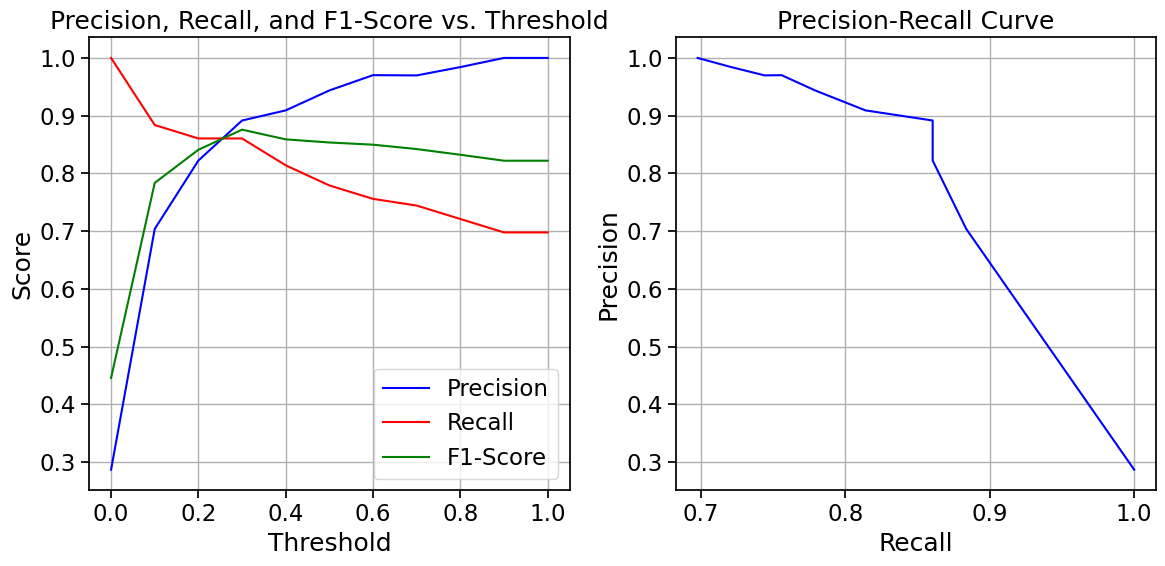
_images/a6d492921992f716b12ae8f0911ff7cf2f2bd6010d36d49ce32237ead9bb135a.png

Choosing the Right Metric#

The choice of evaluation metric depends on the specific problem and the relative costs of different types of errors:

Accuracy: Use when classes are balanced and all types of errors have similar costs
Precision: Use when false positives are more costly (e.g., spam detection)
Recall: Use when false negatives are more costly (e.g., disease detection)
F1-Score: Use when you need a balance between precision and recall

Summary#

In this notebook, we’ve covered:

k-Nearest Neighbors (kNN):
- A non-parametric, instance-based learning algorithm
- Uses distance metrics to find the k closest training examples
- Makes predictions based on majority voting
- The choice of k affects the complexity of decision boundaries
Classification Evaluation Metrics:
- Confusion Matrix: A table showing the counts of true/false positives/negatives
- Accuracy: The proportion of correct predictions
- Precision: The proportion of true positives among predicted positives
- Recall: The proportion of true positives among actual positives
- F1-Score: The harmonic mean of precision and recall
- Precision-Recall Trade-off: Adjusting the decision threshold affects precision and recall

These concepts form the foundation for understanding classification algorithms and evaluating their performance. In the next notebook, we’ll explore Voronoi diagrams and their connection to kNN and Bayesian decision theory.

References#

Duda, R. O., Hart, P. E., & Stork, D. G. (2001). Pattern Classification (2nd ed.). Wiley-Interscience.
Precision and Recall - Wikipedia
Confusion Matrix - Wikipedia
Scikit-learn Documentation - Model Evaluation

k-Nearest Neighbors and Classification Evaluation Metrics

Contents

k-Nearest Neighbors and Classification Evaluation Metrics#

Review of k-Nearest Neighbors (kNN)#

Key Characteristics of kNN:#

The kNN Algorithm (as described in Duda et al.):#

Distance Metrics:#

Observations on kNN Behavior:#

Classification Evaluation Metrics#

Confusion Matrix#

Accuracy#

Precision & Recall#

Precision#

Recall (Sensitivity)#

2.5 F1-Score#

Precision-Recall Trade-off#

Choosing the Right Metric#

Further Reading#

Metrics for Multi-class Classification#

Summary#

References#