Principal Component Analysis, Part 2

A comprehensive guide to understanding PCA from mathematical foundations to practical implementation

---

Principal Component Analysis (PCA) is a fundamental dimensionality reduction technique that identifies an optimal \(r\)-dimensional basis capturing maximum variance in the data. Its mathematical foundation derives from finding orthogonal directions (principal components) that sequentially maximize the projected variance.

Given a centered data matrix \(\mathbf{X}\), we seek unit vectors \(\mathbf{u}\) that maximize the variance of projected data \(\mathbf{X}\mathbf{u}\):

\[\max_{\|\mathbf{u}\|=1} \text{Var}(\mathbf{X}\mathbf{u}) \]

This optimization leads to the key eigenvalue problem:

\[\mathbf{C}\mathbf{u} = \lambda\mathbf{u}\]

where \(\mathbf{C}\) is a covariance matrix.

In the following sections, we will systematically derive the solution to this problem and demonstrate its geometric interpretation.

---

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

# Generate synthetic data with elliptical shape
np.random.seed(42)
n_samples = 100
mean = [0, 0]
cov = [[1, 0.6], [0.6, 0.5]]  # Covariance matrix for elliptical distribution
data = np.random.multivariate_normal(mean, cov, n_samples)

# Center the data
centered_data = data - np.mean(data, axis=0)

# Perform PCA
pca = PCA()
pca.fit(centered_data)
components = pca.components_
explained_variance = pca.explained_variance_ratio_

# Project data onto principal components
projected_data = pca.transform(centered_data)

# Create figure
plt.figure(figsize=(12, 8))

# Plot original data
plt.scatter(centered_data[:, 0], centered_data[:, 1], alpha=0.5, label='Original Data', color='blue')

# Plot principal components as elegant vectors
pc_scale = 2.1  # Scaling factor for PC vectors
plt.quiver(0, 0, components[0,0]*pc_scale, components[0,1]*pc_scale, 
          color='lightcoral', scale=1, scale_units='xy', angles='xy', width=0.002,
          label=f'PC1 (Variance: {100*explained_variance[0]:.1f}%)')
plt.quiver(0, 0, components[1,0]*pc_scale, components[1,1]*pc_scale, 
          color='lightgreen', scale=1, scale_units='xy', angles='xy', width=0.002,
          label=f'PC2 (Variance: {100*explained_variance[1]:.1f}%)')      

# Plot projections onto PC1 (first principal component)
for point in centered_data:
    projection_pc1 = np.dot(point, components[0]) * components[0]
    plt.plot([point[0], projection_pc1[0]], [point[1], projection_pc1[1]], 
             'r--', alpha=0.3, linewidth=0.7)

# Plot projections onto PC2 (second principal component)
for point in centered_data:
    projection_pc2 = np.dot(point, components[1]) * components[1]
    plt.plot([point[0], projection_pc2[0]], [point[1], projection_pc2[1]], 
             'g--', alpha=0.2, linewidth=0.6)

# Plot the projected points on PC1
projected_pc1 = np.dot(projected_data[:, 0][:, np.newaxis], components[0:1, :])
plt.scatter(projected_pc1[:, 0], projected_pc1[:, 1], color='red', alpha=0.7, 
            label='Projections on PC1', s=30)

# Plot the projected points on PC2
projected_pc2 = np.dot(projected_data[:, 1][:, np.newaxis], components[1:2, :])
plt.scatter(projected_pc2[:, 0], projected_pc2[:, 1], color='green', alpha=0.7, 
            label='Projections on PC2', s=30)

# Add annotations and legend
plt.axhline(0, color='black', linestyle='--', alpha=0.2)
plt.axvline(0, color='black', linestyle='--', alpha=0.2)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
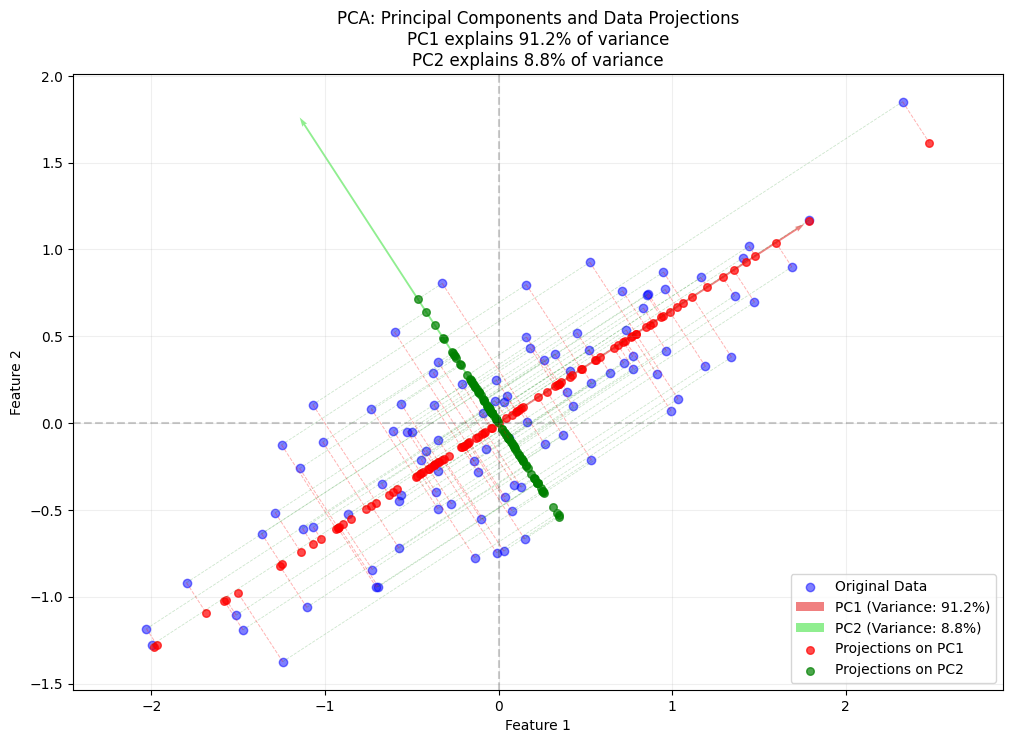
plt.title('PCA: Principal Components and Data Projections\n'
          f'PC1 explains {100*explained_variance[0]:.1f}% of variance\n'
          f'PC2 explains {100*explained_variance[1]:.1f}% of variance')
plt.legend(loc="lower right")
plt.grid(alpha=0.2)
plt.axis('equal')
plt.show()

Linear Algebra Foundations

Data Matrix Representation

A data matrix \(\mathbf{X}\) with \(n\) rows (samples) and \(d\) columns (features) can be written as:

\[\begin{split} \mathbf{X} = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d}\\ x_{21} & x_{22} & \cdots & x_{2d}\\ \vdots & \vdots & \ddots & \vdots\\ x_{n1} & x_{n2} & \cdots & x_{nd} \end{bmatrix} \end{split}\]

Each row \(\mathbf{x}_i = (x_{i1}, x_{i2}, \ldots, x_{id})^T\) represents one sample in \(d\)-dimensional space.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris, make_blobs
from sklearn.decomposition import PCA
import seaborn as sns

# Set style for better plots
plt.style.use('seaborn-v0_8')
np.random.seed(42)

Vector Operations

Dot Product

\[\mathbf{a}^T\mathbf{b} = \sum_{i=1}^m a_i b_i\]

Vector Length (Norm)

\[\|\mathbf{a}\| = \sqrt{\mathbf{a}^T\mathbf{a}} = \sqrt{\sum_{i=1}^m a_i^2}\]

Unit Vector

\[\mathbf{u} = \frac{\mathbf{a}}{\|\mathbf{a}\|}\]

Distance between Vectors

\[\|\mathbf{a} - \mathbf{b}\| = \sqrt{\sum_{i=1}^m (a_i-b_i)^2}\]

Angle between Vectors

\[\cos \theta = \frac{\mathbf{a}^T\mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}\]

# Example: Vector operations
a = np.array([3, 4])
b = np.array([1, 2])

# Dot product
dot_product = np.dot(a, b)
print(f"Dot product: {dot_product}")

# Vector norms
norm_a = np.linalg.norm(a)
norm_b = np.linalg.norm(b)
print(f"Norm of a: {norm_a:.2f}")
print(f"Norm of b: {norm_b:.2f}")

# Angle between vectors
cos_theta = dot_product / (norm_a * norm_b)
theta_rad = np.arccos(cos_theta)
theta_deg = np.degrees(theta_rad)
print(f"Angle between vectors: {theta_deg:.2f} degrees")

Dot product: 11
Norm of a: 5.00
Norm of b: 2.24
Angle between vectors: 10.30 degrees

Vector Projections (Derivation & Geometric Intuition)

Derivation of Projection Formula

We begin with fundamental vector operations to derive the projection formula naturally:

1. Dot Product and Angle Relationship:
   From our previous definitions, we know:

   \[ \mathbf{a}^T \mathbf{b} = \|\mathbf{a}\| \|\mathbf{b}\| \cos \theta \]

   This measures alignment between vectors.

2. Scalar Projection (Length of Shadow):
   The length of \(\mathbf{b}\)’s shadow along \(\mathbf{a}\) is:

   \[ \text{Scalar projection} = \|\mathbf{b}\| \cos \theta = \frac{\mathbf{a}^T \mathbf{b}}{\|\mathbf{a}\|} \]

   For unit vectors, this simplifies to \(\mathbf{a}^T \mathbf{b}\).

3. Vector Projection:
   To get the vector form, we multiply the scalar projection by \(\mathbf{a}\)’s unit vector:

   \[ \mathbf{b}_{\parallel} = \left( \frac{\mathbf{a}^T \mathbf{b}}{\|\mathbf{a}\|} \right) \left( \frac{\mathbf{a}}{\|\mathbf{a}\|} \right) = \frac{\mathbf{a}^T \mathbf{b}}{\|\mathbf{a}\|^2} \mathbf{a} \]

Final Projection Formula

\[ \mathbf{b}_{\parallel} = \left( \frac{\mathbf{a}^T \mathbf{b}}{\|\mathbf{a}\|^2} \right) \mathbf{a} \]

Key Insights:

1. Dot Product Interpretation:

   • The numerator \(\mathbf{a}^T \mathbf{b}\) measures alignment

   • The denominator \(\|\mathbf{a}\|^2\) normalizes for vector length

2. Special Case - Unit Vector: When \(\|\mathbf{a}\|=1\):

   \[ \mathbf{b}_{\parallel} = (\mathbf{a}^T \mathbf{b}) \mathbf{a} \]

3. Geometric Meaning:

   • \(\mathbf{b}_{\parallel}\) is \(\mathbf{b}\)’s shadow on \(\mathbf{a}\)

   • The residual \(\mathbf{b}_{\perp} = \mathbf{b} - \mathbf{b}_{\parallel}\) is orthogonal to \(\mathbf{a}\)

Example

Let \(\mathbf{a} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}\) and \(\mathbf{b} = \begin{bmatrix} 3 \\ 2 \end{bmatrix}\).

• Step 1: Compute \(\mathbf{a}^T \mathbf{b} = 1 \times 3 + 0 \times 2 = 3\).

• Step 2: Compute \(\|\mathbf{a}\|^2 = 1^2 + 0^2 = 1\).

• Step 3: Projection \(\mathbf{b}_{\parallel} = 3\begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 3 \\ 0 \end{bmatrix}\).

• Perpendicular Component: \(\mathbf{b}_{\perp} = \begin{bmatrix} 3 \\ 2 \end{bmatrix} - \begin{bmatrix} 3 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \end{bmatrix}\).

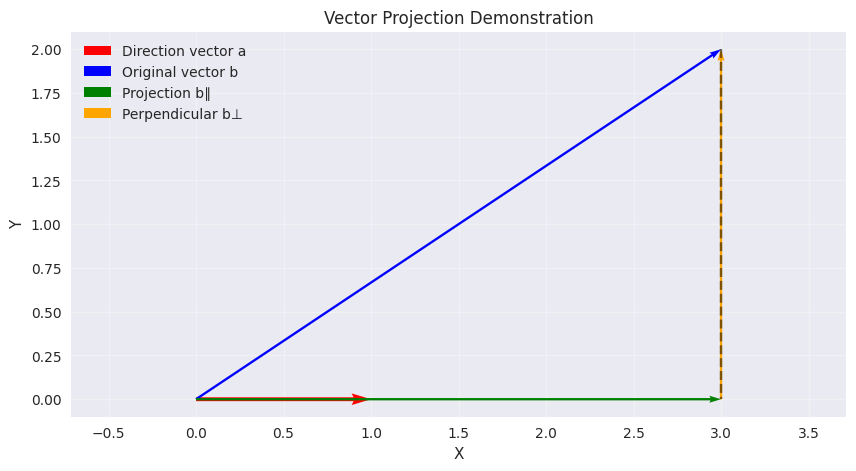
Visualization:

• \(\mathbf{b}_{\parallel}\) retains the x-component of \(\mathbf{b}\) (since \(\mathbf{a}\) is along the x-axis).

• \(\mathbf{b}_{\perp}\) captures the remaining y-component, which is orthogonal to \(\mathbf{a}\).

Next Steps:
We will now see how this projection concept extends to multiple dimensions and leads to the PCA solution via eigenvalue decomposition.

---

# Example: Vector projection
def project_vector(b, a):
    """Project vector b onto vector a"""
    projection = (np.dot(a, b) / np.dot(a, a)) * a
    perpendicular = b - projection
    return projection, perpendicular

# Example vectors
a = np.array([1, 0])  # Direction vector
b = np.array([3, 2])  # Vector to project

b_parallel, b_perp = project_vector(b, a)

print(f"Original vector b: {b}")
print(f"Projection onto a: {b_parallel}")
print(f"Perpendicular component: {b_perp}")
print(f"Verification (should equal b): {b_parallel + b_perp}")

Original vector b: [3 2]
Projection onto a: [3. 0.]
Perpendicular component: [0. 2.]
Verification (should equal b): [3. 2.]

Show code cell source Hide code cell source

plt.rcParams['font.family'] = 'DejaVu Sans'  

# Visualization of vector projection
plt.figure(figsize=(10, 5))

# Plot vectors
plt.quiver(0, 0, a[0], a[1], angles='xy', scale_units='xy', scale=1, color='red', width=0.005, label='Direction vector a')
plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1, color='blue', width=0.003, label='Original vector b')
plt.quiver(0, 0, b_parallel[0], b_parallel[1], angles='xy', scale_units='xy', scale=1, color='green', width=0.003, label='Projection b∥')
plt.quiver(b_parallel[0], b_parallel[1], b_perp[0], b_perp[1], angles='xy', scale_units='xy', scale=1, color='orange', width=0.003, label='Perpendicular b⊥')

# Add dotted line to show projection
plt.plot([b[0], b_parallel[0]], [b[1], b_parallel[1]], 'k--', alpha=0.5)

# Set axis limits with some padding
padding = 0.5
plt.xlim(min(0, b[0], b_parallel[0]) - padding, max(a[0], b[0], b_parallel[0]) + padding)
plt.ylim(min(0, b[1], b_parallel[1]) - padding, max(a[1], b[1], b_parallel[1]) + padding)
# plt.xlim(-0.5, 3.5)
# plt.ylim(-0.5, 2.5)
plt.grid(True, alpha=0.3)
plt.axis('equal')
plt.legend()
plt.title('Vector Projection Demonstration')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

# Print the vectors and their magnitudes
print(f"Vector a: {a}, magnitude: {np.linalg.norm(a):.2f}")
print(f"Vector b: {b}, magnitude: {np.linalg.norm(b):.2f}")
print(f"b_parallel: {b_parallel}, magnitude: {np.linalg.norm(b_parallel):.2f}")
print(f"b_perpendicular: {b_perp}, magnitude: {np.linalg.norm(b_perp):.2f}")

Vector a: [1 0], magnitude: 1.00
Vector b: [3 2], magnitude: 3.61
b_parallel: [3. 0.], magnitude: 3.00
b_perpendicular: [0. 2.], magnitude: 2.00

Basis Transformation

Change of Basis

Any vector \(\mathbf{x}\) can be expressed in terms of a new orthonormal basis \(\{\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_d\}\):

\[\mathbf{x} = a_1\mathbf{u}_1 + a_2\mathbf{u}_2 + \cdots + a_d\mathbf{u}_d = \mathbf{U}\mathbf{a}\]

where \(\mathbf{U}\) is the matrix with columns \(\mathbf{u}_i\) and \(\mathbf{a}\) contains the coordinates in the new basis:

\[\mathbf{a} = \mathbf{U}^T\mathbf{x}\]

# Example: Basis transformation
# Original vector
x = np.array([0.5, 1, 2])

# Standard basis (i, j, k)
standard_basis = np.eye(3)
i = standard_basis[:, 0]
j = standard_basis[:, 1]
k = standard_basis[:, 2]

print(f"Original vector x: {x}")
print(f"In standard basis: {x[0]}i + {x[1]}j + {x[2]}k")

# Create a new orthonormal basis (rotated 45° in xy-plane)
u1 = np.array([1/np.sqrt(2), 1/np.sqrt(2), 0])
u2 = np.array([-1/np.sqrt(2), 1/np.sqrt(2), 0])
u3 = np.array([0, 0, 1])

# New basis matrix
U = np.column_stack([u1, u2, u3])
print(U)

Original vector x: [0.5 1.  2. ]
In standard basis: 0.5i + 1.0j + 2.0k
[[ 0.70710678 -0.70710678  0.        ]
 [ 0.70710678  0.70710678  0.        ]
 [ 0.          0.          1.        ]]

Show code cell source Hide code cell source

# Create 3D plot
fig = plt.figure(figsize=(15, 5))

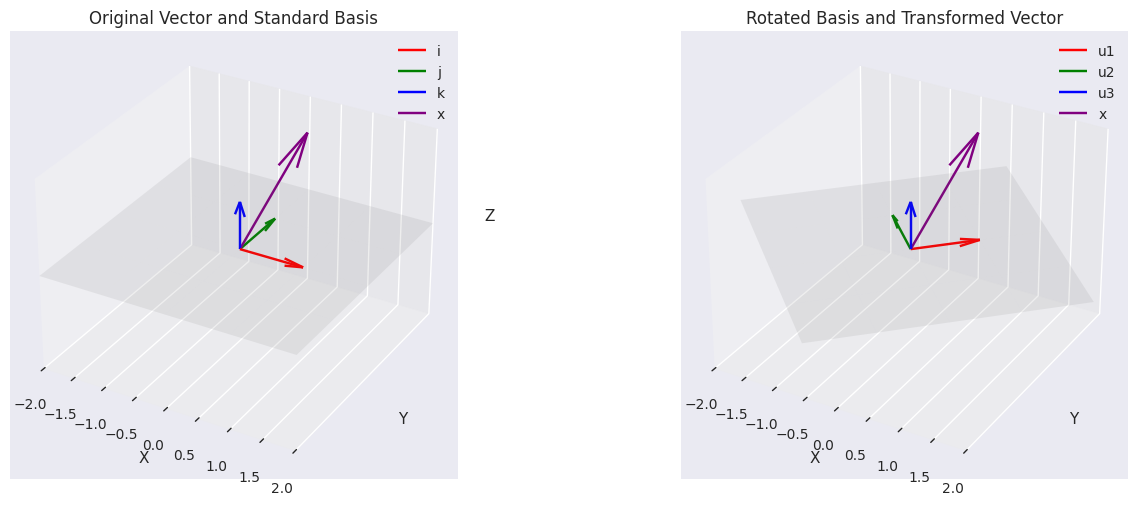
# Plot 1: Original vector and standard basis
ax1 = fig.add_subplot(121, projection='3d')
ax1.set_title('Original Vector and Standard Basis')

# Plot standard basis vectors
ax1.quiver(0, 0, 0, i[0], i[1], i[2], color='r', label='i')
ax1.quiver(0, 0, 0, j[0], j[1], j[2], color='g', label='j')
ax1.quiver(0, 0, 0, k[0], k[1], k[2], color='b', label='k')

# Plot original vector
ax1.quiver(0, 0, 0, x[0], x[1], x[2], color='purple', label='x')

# Plot xy-plane for reference
xx, yy = np.meshgrid(range(-2, 3), range(-2, 3))
zz = np.zeros_like(xx)
ax1.plot_surface(xx, yy, zz, alpha=0.1, color='gray')

# Plot 2: Rotated basis and transformed vector
ax2 = fig.add_subplot(122, projection='3d')
ax2.set_title('Rotated Basis and Transformed Vector')

# Plot rotated basis vectors
ax2.quiver(0, 0, 0, u1[0], u1[1], u1[2], color='r', label='u1')
ax2.quiver(0, 0, 0, u2[0], u2[1], u2[2], color='g', label='u2')
ax2.quiver(0, 0, 0, u3[0], u3[1], u3[2], color='b', label='u3')

# Plot original vector
ax2.quiver(0, 0, 0, x[0], x[1], x[2], color='purple', label='x')

# Plot rotated xy-plane
R = np.array([[1/np.sqrt(2), -1/np.sqrt(2), 0],
              [1/np.sqrt(2), 1/np.sqrt(2), 0],
              [0, 0, 1]])
rotated_points = R @ np.array([xx.flatten(), yy.flatten(), zz.flatten()])
rotated_xx = rotated_points[0].reshape(xx.shape)
rotated_yy = rotated_points[1].reshape(yy.shape)
rotated_zz = rotated_points[2].reshape(zz.shape)
ax2.plot_surface(rotated_xx, rotated_yy, rotated_zz, alpha=0.1, color='gray')

# Set equal aspects and labels
for ax in [ax1, ax2]:
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_xlim([-2, 2])
    ax.set_ylim([-2, 2])
    ax.set_zlim([-2, 2])
    # ax.set_xticks([])  # Disable x-axis numbers
    ax.set_yticks([])  # Disable y-axis numbers
    ax.set_zticks([])  # Disable z-axis numbers
    ax.legend()

plt.tight_layout()
plt.show()

Rotation Matrix Mathematical Foundation

2D Rotation Fundamentals

A rotation matrix transforms vectors by rotating them through a specified angle θ while preserving their length. For a 45° rotation in the xy-plane (θ = π/4 radians), the fundamental rotation matrix is:

\[\begin{split} \mathbf{R}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split}\]

For θ = 45°:

\[ \cos(45°) = \sin(45°) = \frac{1}{\sqrt{2}} \approx 0.7071 \]

Thus, the 45° rotation matrix becomes:

\[\begin{split} \mathbf{R}_{45°} = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split}\]

Basis Transformation

In your code, this rotation matrix defines new basis vectors:

u1 = np.array([1/np.sqrt(2), 1/np.sqrt(2), 0])  # Rotated x-axis
u2 = np.array([-1/np.sqrt(2), 1/np.sqrt(2), 0]) # Rotated y-axis 
u3 = np.array([0, 0, 1])                        # Unchanged z-axis

These form an orthonormal basis:

1. \(\mathbf{u}_1\): Original x-axis rotated 45° counterclockwise

2. \(\mathbf{u}_2\): Original y-axis rotated 45° counterclockwise

3. \(\mathbf{u}_3\): Original z-axis (unchanged)

Key Properties

1. Orthonormality:

   • \(\mathbf{u}_i^T\mathbf{u}_j = \begin{cases} 1 & \text{if } i=j \\ 0 & \text{otherwise} \end{cases}\)

2. Determinant: \(\det(\mathbf{R}) = 1\) (preserves orientation)

3. Inverse: \(\mathbf{R}^{-1} = \mathbf{R}^T\) (transpose reverses rotation)

Vector Transformation

For any vector \(\mathbf{x} = [x,y,z]^T\), the rotated version is:

\[\begin{split} \mathbf{x}' = \mathbf{R}\mathbf{x} = \begin{bmatrix} \frac{x - y}{\sqrt{2}} \\ \frac{x + y}{\sqrt{2}} \\ z \end{bmatrix} \end{split}\]

This matches your basis transformation approach where:

\[ \mathbf{x}' = x\mathbf{u}_1 + y\mathbf{u}_2 + z\mathbf{u}_3 \]

Why This Works

The matrix columns are the transformed standard basis vectors. When we multiply:

\[\begin{split} \mathbf{R}\begin{bmatrix}1\\0\\0\end{bmatrix} = \mathbf{u}_1, \quad \mathbf{R}\begin{bmatrix}0\\1\\0\end{bmatrix} = \mathbf{u}_2, \quad \mathbf{R}\begin{bmatrix}0\\0\\1\end{bmatrix} = \mathbf{u}_3 \end{split}\]

# Transform to new basis
a = U.T @ x

print(f"\nIn new basis: {a[0]:.2f}u1 + {a[1]:.2f}u2 + {a[2]:.2f}u3")

# Verify: transform back to original
x_reconstructed = U @ a
print(f"\nReconstructed x: {x_reconstructed}")
print(f"Reconstruction error: {np.linalg.norm(x - x_reconstructed):.10f}")

In new basis: 1.06u1 + 0.35u2 + 2.00u3

Reconstructed x: [0.5 1.  2. ]
Reconstruction error: 0.0000000000

PCA Mathematical Foundation

Variance Maximization Problem

Principal Component Analysis (PCA) seeks an orthonormal basis \(\{\mathbf{u}_1, \dots, \mathbf{u}_r\}\) that captures maximal variance in the data through sequential optimization:

1. First Principal Component:
   Find unit vector \(\mathbf{u}_1\) maximizing projected variance:

   \[ \max_{\|\mathbf{u}_1\|=1} \text{Var}(\mathbf{X}\mathbf{u}_1) = \max_{\|\mathbf{u}_1\|=1} \frac{1}{n}\|\mathbf{X}\mathbf{u}_1\|^2 \]

2. Subsequent Components:
   Each \(\mathbf{u}_k\) is found by maximizing variance orthogonal to previous components:

   \[ \max_{\|\mathbf{u}_k\|=1, \, \mathbf{u}_k \perp \{\mathbf{u}_1, \dots, \mathbf{u}_{k-1}\}} \text{Var}(\mathbf{X}\mathbf{u}_k) \]

Simply put, the first principal component represents the most significant direction in the data, retaining the maximum variability. Subsequent principal components can be extracted, but each must be orthogonal to the previous components to ensure they capture new and independent information.

Finding the first principal component

We seek a unit vector u that maximizes the variance of the projected data:

\[ \max_{\|\mathbf{u}\|=1} \text{Var}(\mathbf{X}\mathbf{u}) = \max_{\|\mathbf{u}\|=1} \frac{1}{n} \sum_{i=1}^n \left( \mathbf{u}^T \mathbf{x}_i - \mu_{\mathbf{u}} \right)^2 \]

where:

• \(\mu_{\mathbf{u}} = \frac{1}{n} \sum_{i=1}^n \mathbf{u}^T \mathbf{x}_i = \mathbf{u}^T \left( \frac{1}{n} \sum_{i=1}^n \mathbf{x}_i \right) = \mathbf{u}^T \bar{\mathbf{x}}\) is the mean of projected data

Expanding the variance expression:

1. Let \(a_i = \mathbf{u}^T \mathbf{x}_i\) be the projected value

2. The variance becomes:

   \[ \sigma^2_{\mathbf{u}} = \frac{1}{n} \sum_{i=1}^n (a_i - \mu_{\mathbf{u}})^2 = \frac{1}{n} \sum_{i=1}^n \left( \mathbf{u}^T \mathbf{x}_i - \mathbf{u}^T \bar{\mathbf{x}} \right)^2 = \frac{1}{n} \sum_{i=1}^n \left[ \mathbf{u}^T (\mathbf{x}_i - \bar{\mathbf{x}}) \right]^2 \]

Let \(\mathbf{z}_i = \mathbf{x}_i - \bar{\mathbf{x}}\) be the centered data points. Then:

1. Expand using \(\|A\|^2 = A^TA\):

\[ \sigma^2_{\mathbf{u}} = \frac{1}{n} \sum_{i=1}^n (\mathbf{u}^T \mathbf{z}_i)^2 = \frac{1}{n} \sum_{i=1}^n (\mathbf{u}^T \mathbf{z}_i)(\mathbf{z}_i^T \mathbf{u}) \]

2. Apply the identity \(A^TB = B^TA\) to the second term:

\[ = \frac{1}{n} \sum_{i=1}^n \mathbf{u}^T \mathbf{z}_i \mathbf{z}_i^T \mathbf{u} \]

3. Factor out \(\mathbf{u}^T\) and \(\mathbf{u}\):

\[ = \mathbf{u}^T \left( \frac{1}{n} \sum_{i=1}^n \mathbf{z}_i \mathbf{z}_i^T \right) \mathbf{u} \]

4. Recognize the covariance matrix \(\mathbf{C} = \frac{1}{n} \sum_{i=1}^n \mathbf{z}_i \mathbf{z}_i^T\):

\[ = \mathbf{u}^T \mathbf{C} \mathbf{u} \]

5. Express in terms of the centered data matrix \(\mathbf{Z} = [\mathbf{z}_1 \cdots \mathbf{z}_n]^T\):

\[ = \frac{1}{n} \mathbf{u}^T \mathbf{Z}^T \mathbf{Z} \mathbf{u} = \frac{1}{n} \|\mathbf{Z}\mathbf{u}\|^2 \]

Hence the variance of the projected data is:

\[ \boxed{\sigma^2_{\mathbf{u}} = \mathbf{u}^T \mathbf{C} \mathbf{u}} \]

Optimization Problem

We should maximize the projected variance \(\sigma^2_\mathbf{u} = \mathbf{u}^T \mathbf{C} \mathbf{u}\) subject to the constraint \(\mathbf{u}^T\mathbf{u}=1\). This constrained optimization problem can be solved using Lagrange multipliers:

\[ \max_\mathbf{u} J(\mathbf{u}) = \mathbf{u}^T \mathbf{C} \mathbf{u} - \lambda (\mathbf{u}^T\mathbf{u}-1) \]

Deriving the Solution

Taking the derivative with respect to \(\mathbf{u}\) and setting it to zero:

\[ \frac{\partial}{\partial \mathbf{u}} \left(\mathbf{u}^T \mathbf{C} \mathbf{u} - \lambda (\mathbf{u}^T\mathbf{u}-1)\right) = \mathbf{0} \]

\[ 2 \mathbf{C} \mathbf{u} - 2 \lambda \mathbf{u} = \mathbf{0} \]

\[ \mathbf{C} \mathbf{u} = \lambda \mathbf{u} \]

This shows that \(\lambda\) must be an eigenvalue of the covariance matrix \(\mathbf{C}\) with \(\mathbf{u}\) as the corresponding eigenvector.

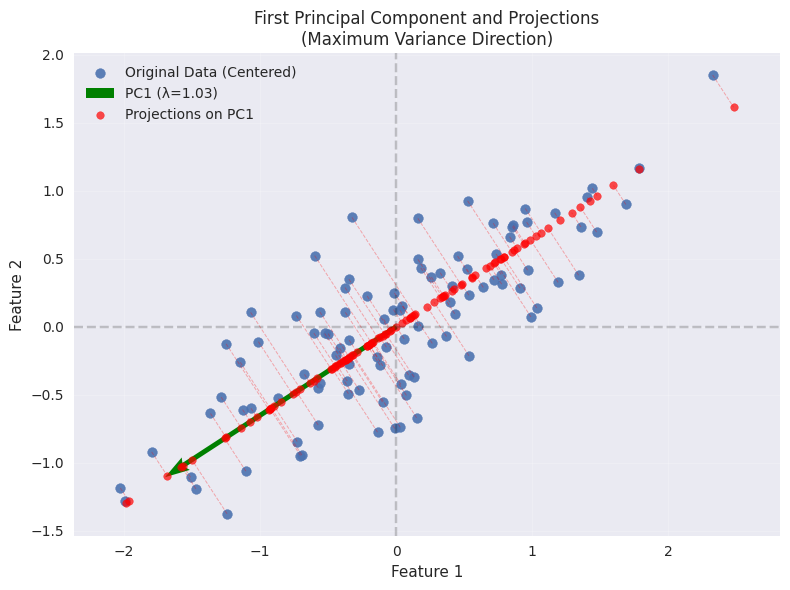
Maximizing the Variance

The projected variance can be expressed as:

\[ \sigma^2_\mathbf{u} = \mathbf{u}^T\mathbf{C}\mathbf{u} = \mathbf{u}^T \lambda \mathbf{u} = \lambda \mathbf{u}^T\mathbf{u} = \lambda \]

Therefore, to maximize the projected variance, we must choose the largest eigenvalue \(\lambda_1\) of \(\mathbf{C}\). The corresponding eigenvector \(\mathbf{u}_1\) gives the direction of maximum variance, known as the first principal component.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt

# Generate synthetic data
np.random.seed(42)
mean = [0, 0]
cov = [[1, 0.6], [0.6, 0.5]]
X = np.random.multivariate_normal(mean, cov, 100)

# Center the data
X_mean = np.mean(X, axis=0)
Z = X - X_mean

# Compute covariance matrix
cov_matrix = np.dot(Z.T, Z) / (len(Z) - 1)

# Compute eigenvalues and eigenvectors
eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)

# Sort by descending eigenvalues
idx = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]

# Extract PC1 (first principal component)
u1 = eigenvectors[:, 0]
λ1 = eigenvalues[0]
print(f"u1 = {u1}, λ1 = {λ1:.2f}")

u1 = [-0.83818843 -0.54538075], λ1 = 1.03

Show code cell source Hide code cell source

# Create figure
plt.figure(figsize=(8, 6))

# Plot original centered data
plt.scatter(Z[:, 0], Z[:, 1], alpha=0.9, label='Original Data (Centered)')

# Plot PC1 direction (scaled by standard deviation)
plt.quiver(0, 0, u1[0]*2*np.sqrt(λ1), u1[1]*2*np.sqrt(λ1), 
           color='green', scale=1, scale_units='xy', angles='xy', width=0.007,
           label=f'PC1 (λ={λ1:.2f})')

# Project data onto PC1
projections = np.outer(Z @ u1, u1)  # Projection vectors

# Plot projections
plt.scatter(projections[:, 0], projections[:, 1], color='red', alpha=0.7,
           s=30, label='Projections on PC1')

# Draw projection lines
for point, proj in zip(Z, projections):
    plt.plot([point[0], proj[0]], [point[1], proj[1]], 
             'r--', alpha=0.3, linewidth=0.7)

# Formatting
plt.axhline(0, color='black', linestyle='--', alpha=0.2)
plt.axvline(0, color='black', linestyle='--', alpha=0.2)
plt.title('First Principal Component and Projections\n(Maximum Variance Direction)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.grid(alpha=0.2)
plt.axis('equal')
plt.tight_layout()
plt.show()

PCA Algorithm

1. Center the data: \(\mathbf{Z} = \mathbf{X} - \mathbf{1}\cdot\mathbf{\mu}^T\)

2. Compute covariance matrix: \(\mathbf{C} = \frac{1}{n}\mathbf{Z}^T\mathbf{Z}\)

3. Find eigenvalues and eigenvectors of \(\mathbf{C}\)

4. Sort eigenvalues in descending order

5. Select top \(r\) eigenvectors as principal components

6. Project data: \(\mathbf{Z}' = \mathbf{Z}\mathbf{U}_r\)

def pca_from_scratch(X, n_components):
    """
    Implement PCA from scratch
    
    Parameters:
    X: data matrix (n_samples, n_features)
    n_components: number of principal components to keep
    
    Returns:
    X_transformed: transformed data
    components: principal components
    eigenvalues: eigenvalues
    mean: data mean
    """
    # Step 1: Center the data
    X_mean = np.mean(X, axis=0)
    Z = X - X_mean
    
    # Step 2: Compute covariance matrix
    n_samples = X.shape[0]
    cov_matrix = np.dot(Z.T, Z) / (n_samples - 1)
    
    # Step 3: Compute eigenvalues and eigenvectors
    eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)
    
    # Step 4: Sort eigenvalues and eigenvectors in descending order
    idx = eigenvalues.argsort()[::-1]
    eigenvalues = eigenvalues[idx]
    eigenvectors = eigenvectors[:, idx]
    
    # Step 5: Select top n_components
    components = eigenvectors[:, :n_components]
    
    # Step 6: Project the data
    X_transformed = np.dot(Z, components)
    
    return X_transformed, components, eigenvalues, X_mean

def reconstruct_data(X_transformed, components, mean):
    """Reconstruct original data from PCA representation"""
    X_reconstructed = np.dot(X_transformed, components.T) + mean
    return X_reconstructed

PCA Workflow: From Single Sample to Full Matrix

Projection & Reconstruction (Single Data Point)

Step 1: Mean-Centering

• Given a raw data vector: \( \mathbf{x} = [x_1, x_2, \dots, x_d]^T \quad \text{(original space)} \)

• Subtract the mean vector: \( \mathbf{z} = \mathbf{x} - \mathbf{\mu} \quad \text{(centered)} \)

  where \(\mathbf{\mu}\) is the mean of all samples.

Step 2: Projection (Dimensionality Reduction)

• Project \(\mathbf{z}\) onto the first \(r\) principal components (PCs) \(\mathbf{u}_1, \dots, \mathbf{u}_r\): \(a_i = \mathbf{u}_i^T \mathbf{z}\) (scalar, projection of \(\mathbf{z}\) onto \(\mathbf{u}_i\))

• The reduced representation (in PCA space) is: \(\mathbf{a} = [a_1, a_2, \dots, a_r]^T \)

Step 3: Reconstruction (Approximation)

• Reconstruct the centered data using the PCs: \( \mathbf{z}' = \sum_{i=1}^r a_i \mathbf{u}_i = a_1 \mathbf{u}_1 + a_2 \mathbf{u}_2 + \dots + a_r \mathbf{u}_r\)

• Add back the mean to return to original space: \( \mathbf{x}_{\text{recon}} = \mathbf{z}' + \mathbf{\mu}\)

Geometric Interpretation

• The reconstruction \(\mathbf{z}'\) is the closest approximation of \(\mathbf{z}\) using only \(r\) directions.

• The error \(\|\mathbf{z} - \mathbf{z}'\|\) comes from discarding the remaining PCs.

---

Generalization to Full Data Matrix

Step 1: Mean-Centering (Matrix Form)

• Original data matrix:

  \[ \mathbf{X} = [\mathbf{x}_1 | \mathbf{x}_2 | \dots | \mathbf{x}_n]^T \quad \text{($n \times d$)} \]

• Mean-centered data:

  \[ \mathbf{Z} = \mathbf{X} - \mathbf{1} \mathbf{\mu}^T \]

  where \(\mathbf{1}\) is a column vector of ones.

Step 2: Projection (PCA Transformation)

• Project all samples onto the first \(r\) PCs (\(\mathbf{U}_r = [\mathbf{u}_1 | \dots | \mathbf{u}_r]\)):

  \[ \mathbf{A} = \mathbf{Z} \mathbf{U}_r \quad \text{($n \times r$ matrix of PCA coordinates)} \]

  • Each row of \(\mathbf{A}\) contains the reduced representation of a sample.

Step 3: Reconstruction (Matrix Form)

• Reconstruct the centered data:

  \[ \mathbf{Z}' = \mathbf{A} \mathbf{U}_r^T = \sum_{i=1}^r \mathbf{a}_i \mathbf{u}_i^T \]

  • \(\mathbf{a}_i\) = \(i\)-th column of \(\mathbf{A}\) (scores for PC \(i\)).

  • Each term \(\mathbf{a}_i \mathbf{u}_i^T\) is a rank-1 matrix.

• Return to original space:

  \[ \mathbf{X}_{\text{recon}} = \mathbf{Z}' + \mathbf{1} \mathbf{\mu}^T \]

---

Connection to Python Implementation

Projection (Dimensionality Reduction)

X_transformed = Z @ U_r  # ≡ Z U_r (n × r matrix)

Reconstruction

Z_recon = X_transformed @ U_r.T  # ≡ A U_r^T (n × d)
X_recon = Z_recon + mean        # Add back mean

---

Key Takeaways

1. Single Sample → Full Matrix:

   • Start with a single vector to understand projection/reconstruction.

   • Generalize to the full dataset using matrix operations.

2. Lossy Compression:

   • Keeping only \(r < d\) PCs means the reconstruction is approximate.

   • The error depends on the discarded eigenvalues.

3. PCA as a Rotation:

   • Projection = Rotate data to align with maximum variance directions.

   • Reconstruction = Rotate back, using only the most important directions.

Equivalence of PCA’s Two Optimization Perspectives and Error Analysis (Further Reading)

PCA can be derived from two equivalent perspectives:

1. Variance Maximization: Find directions that maximize projected variance.

2. Reconstruction Error Minimization: Find directions that minimize the mean squared reconstruction error.

We’ll prove their equivalence mathematically and analyze the error.

---

1. Variance Maximization Formulation

Goal: Find unit vector \( \mathbf{u} \) that maximizes the variance of projected data:

\[ \max_{\mathbf{u}} \frac{1}{n} \sum_{j=1}^n (\mathbf{u}^T \mathbf{z}_j)^2 \quad \text{subject to} \quad \|\mathbf{u}\| = 1. \]

• The solution is the eigenvector of \( \mathbf{Z}^T \mathbf{Z} \) with largest eigenvalue.

---

2. Reconstruction Error Minimization

Goal: Find \( \mathbf{u} \) that minimizes the MSE between original data \( \mathbf{z}_j \) and its reconstruction \( \mathbf{z}_j' = (\mathbf{u}^T \mathbf{z}_j)\mathbf{u} \):

\[ \min_{\mathbf{u}} \frac{1}{n} \sum_{j=1}^n \|\mathbf{z}_j - (\mathbf{u}^T \mathbf{z}_j)\mathbf{u}\|^2 \quad \text{subject to} \quad \|\mathbf{u}\| = 1. \]

---

3. Proof of Equivalence

Expand the reconstruction error:

\[ \|\mathbf{z}_j - (\mathbf{u}^T \mathbf{z}_j)\mathbf{u}\|^2 = \|\mathbf{z}_j\|^2 - (\mathbf{u}^T \mathbf{z}_j)^2. \]

Thus, the MSE becomes:

\[ \text{MSE} = \frac{1}{n} \sum_{j=1}^n \|\mathbf{z}_j\|^2 - \frac{1}{n} \sum_{j=1}^n (\mathbf{u}^T \mathbf{z}_j)^2. \]

Key Observations:

1. The term \( \frac{1}{n} \sum \|\mathbf{z}_j\|^2 \) is constant (total variance in data).

2. Minimizing MSE is equivalent to maximizing \( \frac{1}{n} \sum (\mathbf{u}^T \mathbf{z}_j)^2 \) (projected variance).

---

4. Error Analysis in PCA

Projection and Residual Components

For a data point \( \mathbf{z}_j \) (centered) and its reconstruction \( \mathbf{z}_j' \) using \( r \) PCs:

\[ \mathbf{z}_j = \underbrace{\sum_{i=1}^r (\mathbf{u}_i^T \mathbf{z}_j)\mathbf{u}_i}_{\text{Reconstruction } \mathbf{z}_j'} + \underbrace{\sum_{i=r+1}^d (\mathbf{u}_i^T \mathbf{z}_j)\mathbf{u}_i}_{\text{Error } \mathbf{\epsilon}_j} \]

• Error vector: \( \mathbf{\epsilon}_j = \mathbf{z}_j - \mathbf{z}_j' = \sum_{i=r+1}^d (\mathbf{u}_i^T \mathbf{z}_j)\mathbf{u}_i \).

---

Mean Squared Error (MSE) Derivation

The total MSE across all samples is:

\[ \text{MSE} = \frac{1}{n} \sum_{j=1}^n \|\mathbf{\epsilon}_j\|^2 = \frac{1}{n} \sum_{j=1}^n \left\| \sum_{i=r+1}^d (\mathbf{u}_i^T \mathbf{z}_j)\mathbf{u}_i \right\|^2. \]

\[ \|\mathbf{\epsilon}_j\|^2 = \sum_{i=r+1}^d (\mathbf{u}_i^T \mathbf{z}_j)^2 \underbrace{\|\mathbf{u}_i\|^2}_{=1} = \sum_{i=r+1}^d (\mathbf{u}_i^T \mathbf{z}_j)^2 \]

\[ \text{MSE} = \frac{1}{n} \sum_{j=1}^n \sum_{i=r+1}^d (\mathbf{u}_i^T \mathbf{z}_j)^2 = \sum_{i=r+1}^d \left( \frac{1}{n} \sum_{j=1}^n (\mathbf{u}_i^T \mathbf{z}_j)^2 \right). \]

---

Link to Eigenvalues

By definition, the variance along \( \mathbf{u}_i \) is:

\[ \lambda_i = \frac{1}{n} \sum_{j=1}^n (\mathbf{u}_i^T \mathbf{z}_j)^2. \]

Thus:

\[ \text{MSE} = \sum_{i=r+1}^d \lambda_i. \]

---

5. Conclusion and Summary

• Dual Formulations: Variance maximization and error minimization are equivalent in PCA.

• Eigenvalue Interpretation: The MSE equals the sum of discarded eigenvalues because:

  • Each \( \lambda_i \) represents variance along PC \( \mathbf{u}_i \).

  • Discarding PCs \( r+1 \) to \( d \) loses exactly \( \sum_{i=r+1}^d \lambda_i \) variance.

• Optimality: PCA’s solution simultaneously maximizes preserved variance and minimizes reconstruction error.

Key Relationships:

Concept	Formula	Interpretation
Projection	\( \mathbf{z}_j' = \sum_{i=1}^r (\mathbf{u}_i^T \mathbf{z}_j)\mathbf{u}_i \)	Reconstruction using top \( r \) PCs
Error	\( \mathbf{\epsilon}_j = \sum_{i=r+1}^d (\mathbf{u}_i^T \mathbf{z}_j)\mathbf{u}_i \)	Residual from discarded PCs
MSE	\( \text{MSE} = \sum_{i=r+1}^d \lambda_i \)	Sum of variances of discarded PCs

Examples and Applications

Iris Dataset Example

Show code cell source Hide code cell source

# Load the Iris dataset
iris = load_iris()
X_iris = iris.data
y_iris = iris.target
feature_names = iris.feature_names

print(f"Original data shape: {X_iris.shape}")
print(f"Features: {feature_names}")

# Apply PCA
X_pca, components, eigenvalues, mean = pca_from_scratch(X_iris, n_components=2)

# Calculate explained variance ratio
total_var = eigenvalues.sum()
explained_var_ratio = eigenvalues[:2] / total_var

print(f"\nExplained variance ratio:")
print(f"PC1: {explained_var_ratio[0]:.3f} ({explained_var_ratio[0]*100:.1f}%)")
print(f"PC2: {explained_var_ratio[1]:.3f} ({explained_var_ratio[1]*100:.1f}%)")
print(f"Total: {explained_var_ratio.sum():.3f} ({explained_var_ratio.sum()*100:.1f}%)")

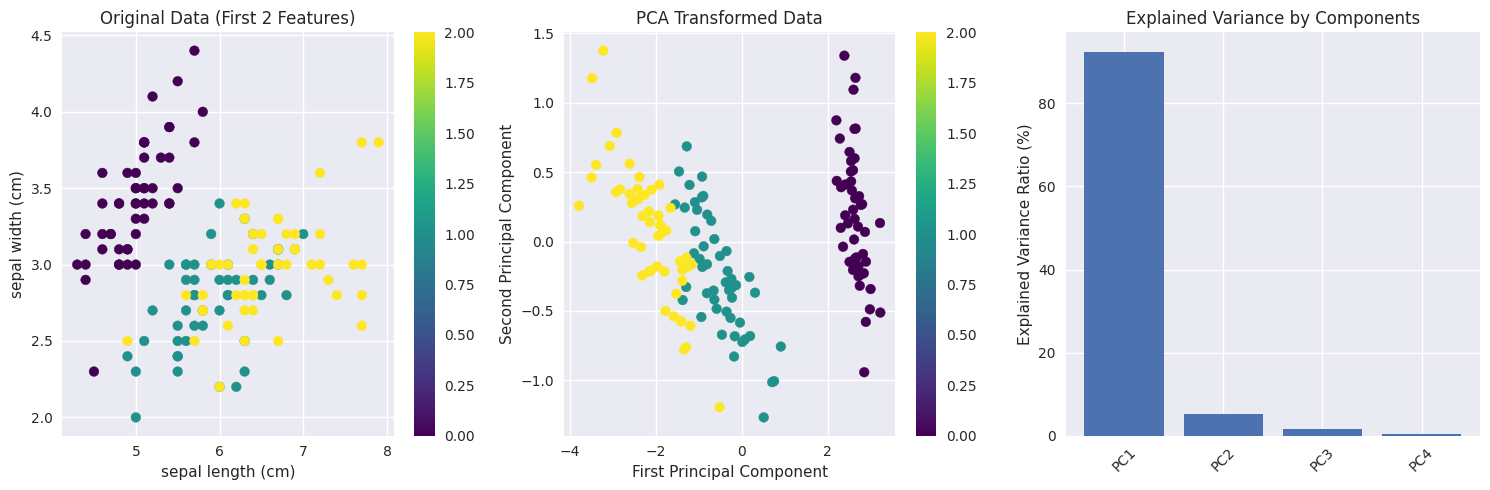
Original data shape: (150, 4)
Features: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']

Explained variance ratio:
PC1: 0.925 (92.5%)
PC2: 0.053 (5.3%)
Total: 0.978 (97.8%)

Show code cell source Hide code cell source

# Visualize the results
plt.figure(figsize=(15, 5))

# Plot 1: Original data (first two features)
plt.subplot(1, 3, 1)
scatter = plt.scatter(X_iris[:, 0], X_iris[:, 1], c=y_iris, cmap='viridis')
plt.xlabel(feature_names[0])
plt.ylabel(feature_names[1])
plt.title('Original Data (First 2 Features)')
plt.colorbar(scatter)

# Plot 2: PCA transformed data
plt.subplot(1, 3, 2)
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_iris, cmap='viridis')
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA Transformed Data')
plt.colorbar(scatter)

# Plot 3: Explained variance
plt.subplot(1, 3, 3)
plt.bar(['PC1', 'PC2', 'PC3', 'PC4'], eigenvalues/total_var * 100)
plt.ylabel('Explained Variance Ratio (%)')
plt.title('Explained Variance by Components')
plt.xticks(rotation=45)

plt.tight_layout()
plt.show()

Reconstruction Error Analysis

Show code cell source Hide code cell source

# Analyze reconstruction error for different numbers of components
n_features = X_iris.shape[1]
reconstruction_errors = []

for n_comp in range(1, n_features + 1):
    X_pca_temp, components_temp, _, mean_temp = pca_from_scratch(X_iris, n_comp)
    X_reconstructed = reconstruct_data(X_pca_temp, components_temp, mean_temp)
    
    # Calculate mean squared error
    mse = np.mean((X_iris - X_reconstructed) ** 2)
    reconstruction_errors.append(mse)

plt.figure(figsize=(10, 6))
plt.plot(range(1, n_features + 1), reconstruction_errors, 'bo-')
plt.xlabel('Number of Principal Components')
plt.ylabel('Mean Squared Reconstruction Error')
plt.title('Reconstruction Error vs Number of Components')
plt.grid(True, alpha=0.3)
plt.xticks(range(1, n_features + 1))

for i, error in enumerate(reconstruction_errors):
    plt.annotate(f'{error:.4f}', (i+1, error), textcoords="offset points", xytext=(0,10), ha='center')

plt.show()

print("Reconstruction errors:")
for i, error in enumerate(reconstruction_errors):
    print(f"{i+1} components: MSE = {error:.6f}")

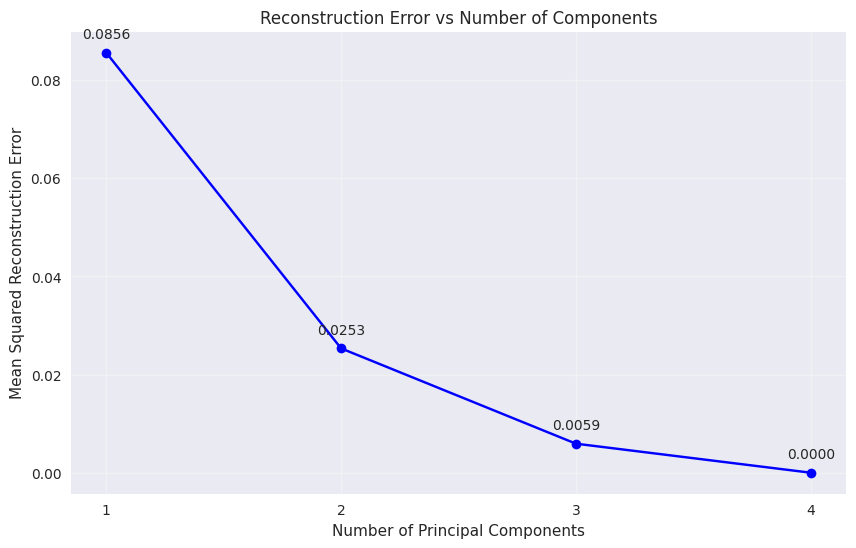
Reconstruction errors:
1 components: MSE = 0.085604
2 components: MSE = 0.025341
3 components: MSE = 0.005919
4 components: MSE = 0.000000

High-Dimensional Data Example

Show code cell source Hide code cell source

# Generate high-dimensional data with intrinsic low-dimensional structure
np.random.seed(42)
n_samples = 200
n_features = 50
n_informative = 3  # True dimensionality

# Generate data with only 3 informative dimensions
X_high_dim = np.random.randn(n_samples, n_informative)

# Create a random mixing matrix to embed in high-dimensional space
mixing_matrix = np.random.randn(n_informative, n_features)
X_mixed = X_high_dim @ mixing_matrix

# Add some noise
noise_level = 0.1
X_noisy = X_mixed + noise_level * np.random.randn(n_samples, n_features)

print(f"Generated data shape: {X_noisy.shape}")
print(f"True intrinsic dimensionality: {n_informative}")

# Apply PCA
X_pca_high, components_high, eigenvalues_high, mean_high = pca_from_scratch(X_noisy, n_components=10)

# Calculate cumulative explained variance
total_var_high = eigenvalues_high.sum()
explained_var_ratio_high = eigenvalues_high / total_var_high
cumulative_var = np.cumsum(explained_var_ratio_high)

print(f"\nExplained variance by first 10 components:")
for i in range(10):
    print(f"PC{i+1}: {explained_var_ratio_high[i]:.3f} (cumulative: {cumulative_var[i]:.3f})")

Generated data shape: (200, 50)
True intrinsic dimensionality: 3

Explained variance by first 10 components:
PC1: 0.420 (cumulative: 0.420)
PC2: 0.342 (cumulative: 0.763)
PC3: 0.234 (cumulative: 0.997)
PC4: 0.000 (cumulative: 0.997)
PC5: 0.000 (cumulative: 0.997)
PC6: 0.000 (cumulative: 0.997)
PC7: 0.000 (cumulative: 0.997)
PC8: 0.000 (cumulative: 0.998)
PC9: 0.000 (cumulative: 0.998)
PC10: 0.000 (cumulative: 0.998)

Show code cell source Hide code cell source

# Visualize the explained variance
plt.figure(figsize=(12, 5))

# Plot 1: Individual explained variance
plt.subplot(1, 2, 1)
plt.bar(range(1, 11), explained_var_ratio_high[:10] * 100)
plt.xlabel('Principal Component')
plt.ylabel('Explained Variance Ratio (%)')
plt.title('Individual Explained Variance')
plt.xticks(range(1, 11))

# Plot 2: Cumulative explained variance
plt.subplot(1, 2, 2)
plt.plot(range(1, 11), cumulative_var[:10] * 100, 'bo-')
plt.axhline(y=95, color='r', linestyle='--', label='95% threshold')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance (%)')
plt.title('Cumulative Explained Variance')
plt.legend()
plt.grid(True, alpha=0.3)
plt.xticks(range(1, 11))

plt.tight_layout()
plt.show()

# Find number of components for 95% variance
n_components_95 = np.argmax(cumulative_var >= 0.95) + 1
print(f"\nNumber of components needed for 95% variance: {n_components_95}")
print(f"This is close to the true intrinsic dimensionality of {n_informative}")

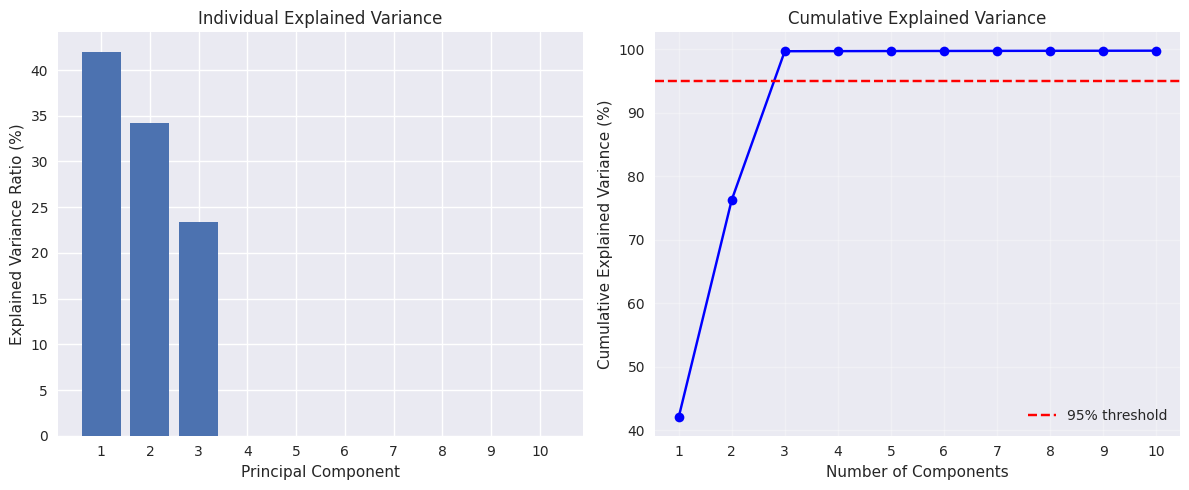
Number of components needed for 95% variance: 3
This is close to the true intrinsic dimensionality of 3

Comparison with Scikit-learn

Show code cell source Hide code cell source

# Compare our implementation with scikit-learn
from sklearn.decomposition import PCA as SklearnPCA

# Our implementation
X_pca_ours, components_ours, eigenvalues_ours, mean_ours = pca_from_scratch(X_iris, n_components=2)

# Scikit-learn implementation
pca_sklearn = SklearnPCA(n_components=2)
X_pca_sklearn = pca_sklearn.fit_transform(X_iris)

print("Comparison of implementations:")
print(f"Our explained variance ratio: {eigenvalues_ours[:2]/eigenvalues_ours.sum()}")
print(f"Sklearn explained variance ratio: {pca_sklearn.explained_variance_ratio_}")

# The signs of eigenvectors might be different, but the results should be equivalent
print(f"\nMean absolute difference in transformed data: {np.mean(np.abs(np.abs(X_pca_ours) - np.abs(X_pca_sklearn))):.10f}")

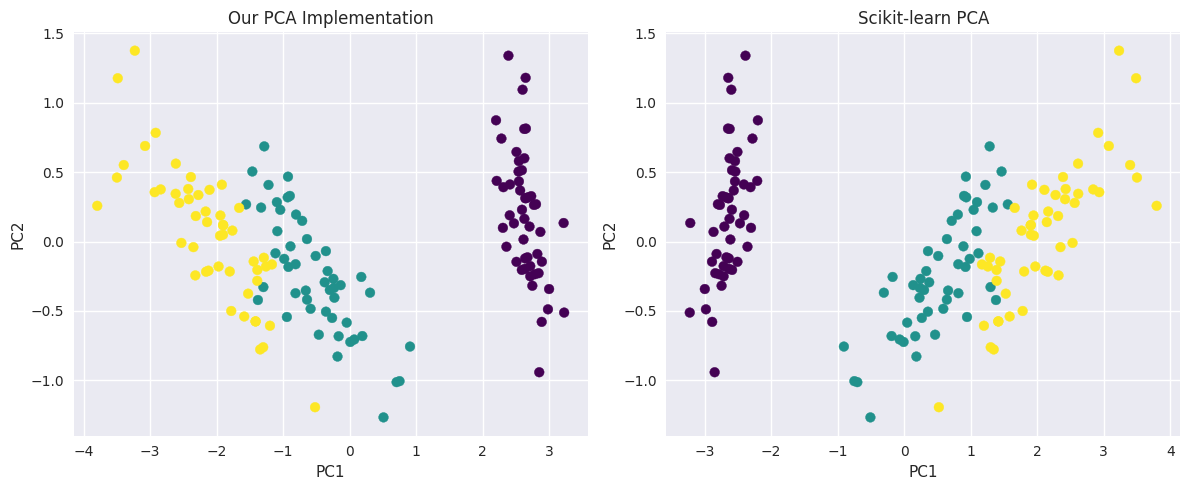
# Visualize both results
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.scatter(X_pca_ours[:, 0], X_pca_ours[:, 1], c=y_iris, cmap='viridis')
plt.title('Our PCA Implementation')
plt.xlabel('PC1')
plt.ylabel('PC2')

plt.subplot(1, 2, 2)
plt.scatter(X_pca_sklearn[:, 0], X_pca_sklearn[:, 1], c=y_iris, cmap='viridis')
plt.title('Scikit-learn PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')

plt.tight_layout()
plt.show()

Comparison of implementations:
Our explained variance ratio: [0.92461872 0.05306648]
Sklearn explained variance ratio: [0.92461872 0.05306648]

Mean absolute difference in transformed data: 0.0000000000

Some of my previous papers are about PCA, including [AFF07, AF22, AP15, FMA08]

Summary

This tutorial covered:

1. Linear Algebra Foundations: Vector operations, norms, and angles

2. Vector Projections: Mathematical foundation for dimensionality reduction

3. Basis Transformation: How to represent data in different coordinate systems

4. PCA Theory: Variance maximization and eigenvalue decomposition

5. Implementation: Step-by-step PCA algorithm from scratch

6. Applications: Real examples with Iris dataset and high-dimensional data

Key Takeaways:

• PCA finds directions of maximum variance in the data

• Principal components are eigenvectors of the covariance matrix

• The eigenvalues represent the amount of variance captured by each component

• PCA provides optimal linear dimensionality reduction in terms of reconstruction error

• The number of components can be chosen based on desired explained variance threshold